Мы уже обсуждали, как встроить правило Sigma в YAML-файл, который следует стандарту или спецификации, установленной авторами Sigma. Он также доступен на странице GitHub. Чтобы обобщить эту информацию — следующие пункты являются хорошим эмпирическим правилом:
Все, что вы хотели знать о Sigma-правилах. Часть 1
При разработке продуктов и накоплении опыта мы руководствуемся в первую очередь желанием повысить безопасность предприятия. Однако наши исследования обусловлены не только интересами клиентов. В течение некоторого времени у нас было желание проводить исследования для сообщества безопасности на добровольной основе, и мы активно этим занимаемся: публикуем сенсационные открытия сетевых атак в Twitter, предоставляем правила анализа трафика для сервиса ANY.RUN и добавляем новые правила в набор правил ETOpen. Существует множество проектов с открытым исходным кодом, в которые мы можем отправить запрос на исправление ошибок, но до недавнего времени мы не могли получить трассировку хоста.
И тут мы узнали, что группа энтузиастов решила организовать двухнедельный спринт для написания правил для Sigma — проекта, созданного для разработки унифицированного формата правил для SIEM-систем и поддерживаемого более чем 140 пользователями. Новость о мероприятии была интересна нам, поскольку мы, как поставщик SIEM, внимательно следим за развитием сообщества.
Представьте себе наше удивление, когда организаторы связались с нами и пригласили команду Центра безопасности PT Expert принять участие в спринте! Участники мероприятия основали Open Security Collaborative Development (OSCD), международную инициативу IT-экспертов по распространению знаний и улучшению компьютерной безопасности в целом. Мы были рады принять участие, чтобы использовать наш опыт на благо общей безопасности. Часть вторая, часть третья
Как появилась эта статья
Когда мы начали писать правила, мы поняли, что исчерпывающего описания синтаксиса правил Sigma не существует, тем более на русском языке. Основными источниками знаний являются GitHub и личный опыт. Есть несколько хороших статей (на русском и английском языках), но их фокус смещен от создания правил к анализу области применения правил Sigma или созданию конкретного правила. Мы решили облегчить новичкам начало работы с Sigma, поделиться собственным опытом, собрать в одном месте информацию о ее составлении и особенностях использования. И конечно, мы надеемся, что это поможет расширить инициативу OSCD и создать более крупное сообщество.
Поскольку материала очень много, мы решили сделать это в серии из трех статей:
- Краткое введение, пример создания простого правила и описание источников событий (и того, что вы сейчас читаете).
- Описание логики обнаружения. Это самая важная часть синтаксиса, которую необходимо знать, чтобы понимать существующие правила и писать свои собственные правила.
- Описание мета-информации (атрибуты, которые являются информативными или подструктурными по своей природе, такие как описание или идентификатор) и коллекции правил.
Что такое формат Sigma и зачем он нужен
Sigma — это единый формат для описания правил обнаружения на основе данных из протоколов. Sigma позволяет написать правило один раз с единым синтаксисом, а затем использовать специальный конвертер для получения правила в синтаксисе поддерживаемого SIEM. Помимо составления запросов из различных SIEM, поддерживаются следующие типы запросов:
- Запрос в Elasticsearch,
- Запрос ElasticSearch; Строка для запуска утилиты grep с необходимыми параметрами,
- Строка запроса PowerShell для доступа к журналам аудита Windows.
Общий формат описания обнаружений на основе протоколов облегчает обмен знаниями, разработку решений безопасности с открытым исходным кодом и помогает сообществу безопасности бороться с новыми угрозами.
Из приведенной выше выдержки видно, что правило использует журналы Sysmon и стандартные журналы Windows, а именно eventID 1 или 4688, в качестве источников данных. Это непосредственно те источники данных, которые Plaso исследовал в первой статье и затем загрузил в ES в этом формате.
Правило трех сигм
Математическое ожидаемое значение — это среднее значение случайной величины. Это называется \(\mu\).
Стандартное отклонение является наиболее распространенным показателем дисперсии значения относительно ожидаемого значения. Он обозначается символом \(\Sigma\), который произносится как «сигма».
Правило трех сигм гласит, что в нормальном распределении почти все значения имеют вероятность 0,9973 в пределах трех сигм в каждом направлении от ожидаемого значения, т.е. в диапазоне \(\links\mu-3\sigma;\mu+3\sigma
ight\).
Осторожно. Если преподаватель обнаружит плагиат в вашей работе, у вас будут серьезные неприятности (вплоть до исключения). Если вы не можете написать работу самостоятельно, закажите ее здесь.
Около 99,7% всех оценок находятся в пределах трех сигм от ожидаемого значения, около 95% — в пределах двух сигм, и около 68% оценок — в пределах одной сигмы.
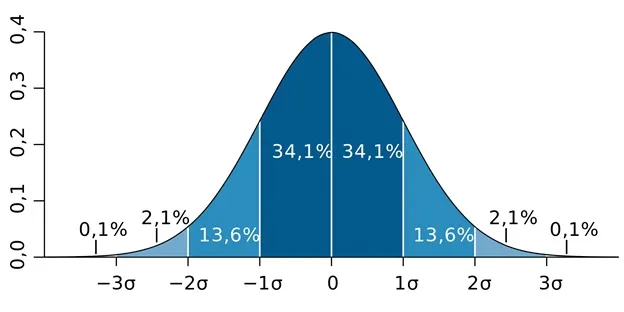
Нормальное распределение случайной величины
Эти значения, превышающие 3 сигмы, обычно считаются большими ошибками. Большое количество таких ошибок может указывать на то, что распределение на самом деле не является нормальным. Это практическое использование правила 3 сигм.
Нормальное распределение (гауссово распределение) — это распределение вероятности, функция плотности которого равна гауссовой функции.
где \(\mu\) — ожидаемое значение, \(\sigma\) — стандартное отклонение и \(\sigma^2\) — дисперсия распределения.
Функция плотности — это функция, которая характеризует относительную вероятность реализации определенных значений одной или нескольких случайных величин.
Другими словами, функция плотности показывает вероятность того, что случайная величина равна определенному значению. Чем «выше» значение на оси порядка, тем больше вероятность того, что случайная величина равна заданному значению на оси бездны. Поэтому на графике нормального распределения значение, совпадающее с точкой максимума, является наиболее вероятным. Значения у «основания» графика, т.е. самые низкие на оси Y, менее вероятны.
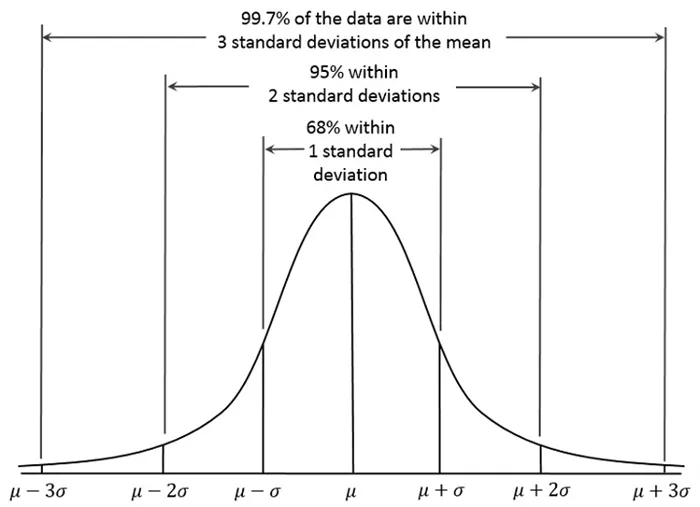
Нормальное распределение величины центрируется и нормализуется.
График нормального распределения тесно связан с центральной предельной теоремой (ЦПТ), которая утверждает, что сумма достаточно большого числа слабо зависимых случайных величин имеет распределение, приближенное к нормальному распределению.
Примеры решения задач
Нормальное распределение — это не абстрактная концепция. Она соответствует определенным характеристикам живых организмов в популяции, их отклонению от цели при стрельбе, их измерениям и их ошибкам. Во всех этих случаях чаще всего встречается группа близко расположенных друг к другу значений, но есть колебания как в большую, так и в меньшую сторону.
Давайте рассмотрим несколько простых задач на применение правила 3 сигм.
Проблема 1
Имеется выборка жителей богатого дома. Средняя заработная плата жителей составляет 150 000 рублей; стандартное отклонение — 20 000 рублей. Определите, какие жители с зарплатой вряд ли будут жить в этом доме: A) 205 000 рублей, B) 95 000, C) 230 000, D) 87 000.
Решение
Чтобы решить эту проблему, необходимо определить верхнюю и нижнюю границы возможных зарплат в доме. Для этого мы используем правило 3 сигм.
Значения A, B находятся в диапазоне \(\left90\;000;\;210\;000
ight\). Значения C, D не попадают в этот диапазон и поэтому являются приблизительными погрешностями, которые вы ищете.
Имеется выборка жителей богатого дома. Средняя заработная плата жителей составляет 150 000 рублей; стандартное отклонение — 20 000 рублей. Определите, какие жители с зарплатой вряд ли будут жить в этом доме: A) 205 000 рублей, B) 95 000, C) 230 000, D) 87 000.
Завод производит партию из 100 цилиндрических деталей. Диаметр каждой детали является случайной величиной, распределенной по нормальному закону. Математическое ожидаемое значение составляет 65 мм, а стандартное отклонение — 0,9 мм. Для упаковки партии используются ящики шириной 6600 мм. Компоненты расположены в ряд. Если компоненты не помещаются в одну коробку, необходимо взять другую коробку. Определите вероятность того, что потребуется только одна коробка.
Решение есть.
Поскольку диаметр каждой части распределен нормально, общий диаметр также распределен нормально.