* У одного человека две руки. Пальцы каждой руки состоят из трех фаланг (за исключением большого пальца). На каждой руке по пять пальцев. Другими словами, всего их 10, но за исключением двух двухмерных больших пальцев, только восемь пальцев созданы в соответствии с принципом золотого сечения. Все эти числа 2, 3, 5 и 8 являются числами последовательности Фибоначчи.
Найти золотую середину, или тайны золотого сечения
Число, называемое золотым сечением или серединой (PHI), является одним из самых загадочных терминов в математике и физике. Многие люди никогда не задумываются об этом, но интересно отметить, что это так часто встречается в повседневной жизни, особенно когда речь идет о числах последовательности Фибоначчи. Даже люди, не знакомые с золотым перекрестком, могут увидеть его, не понимая. Был проведен эксперимент. Людям показывают случайные лица и просят назвать наиболее привлекательное. Это были лица, где золотые разрезы находились между разными размерами ширины лица, глаз, бровей и носа. Поэтому инстинктивно человек воспринимает подход к пропорциям как идеальный.
Это пропорция, полученная в результате деления на крайние и промежуточные соотношения. Его также называют гармоничным разделением. Как рассчитывается золотое сечение? В математическом смысле это причина двух величин A и B. Известно, что при A>b выполняется следующее равенство: a/b = (a+b)/a. Если мы говорим, что A и B являются частью отрезка, то можно сказать: небольшая часть слово для небольшой части причина для большей части равный. Золотое пересечение символизируется 21 буквой греческого алфавита, φ (f).
Это число так же мало, как и P, и указывает причину, по которой окружность круга относится к его диаметру. Это выглядит следующим образом: 1,6180339887498948420 … Результат округляется до 1,618.
История золотого сечения
Это значение имеет разные названия. Среди них — божественная пропорция и асимметричная симметрия. Считается, что Пифагор ввел метод золотого сечения в науку в 6 веке до нашей эры. Он научился этому у египтян и вавилонян. Кроме того, о том, что они использовали соотношение золотых делений, свидетельствуют пропорции пирамид, храмов, рельефов, предметов быта и драгоценностей.
Это правило встречается и в других древних сооружениях. Например, высота пирамиды Гизы составляет 146,6 метра, а стороны основания достигают 230,5 метра. Вычисляя соотношение между длиной и высотой сторон, получаем 1,5717. f. Применяя правила Золотого креста, он создал скульптуру Парфенона. Золотое сечение Платон назвал глобальным звеном в математических отношениях. Евклид увидел золотое пересечение пентаграмм еще в 4 веке до нашей эры.
Последовательность Фибоначчи напрямую связана с этим значением. Известные математики создали последовательность чисел, и если взять два последовательных числа, то причина очень близка к F. По мере увеличения числа соотношение все ближе и ближе к 1,618. Например, если вы получите 3 и 5, то соотношение будет 1,666; если вы получите 13 и 21, то будет 1,625. Равные значения f дают отношение 144 к 233.
«Золотые» фигуры
Начало золотого пересечения используется для построения геометрической фигуры. Считается, что сфотографированные таким образом фигуры выглядят красивее. Это подтверждается повторными экспериментами. Внимание испытуемых больше привлекают такие формы.

Самый простой пример — прямоугольник, где соотношение сторон указывает на величину F. Другой прекрасный пример — правильный пятиугольник. Все его диагонали разделены на отрезки, соединенные друг с другом в золотой пропорции, каждый конец — золотой треугольник. В вершине такого треугольника образуется угол в 36 градусов, а низ делит стороны на золотые отрезки. Внутри пятиугольника делается клёпка.
Древнегреческий ученый Архимед первым заметил, что если из золотого прямоугольника последовательно вырезать квадрат, а противоположные точки соединить четвертью окружности, то получится изящная спираль.
Аналогичный принцип используется, например, для расчета правильного положения втулки с линейными размерами. На этой схеме показано, где именно нужно расположить кусты по отношению к деревьям и пруду. Расстояние между объектами составляет 10 метров. Умножение 10 на 0,618 дает расстояние от дерева до будущего куста.
Как построить прямоугольник с идеальными пропорциями
Чтобы применить полученную информацию на практике, нужно как-то научиться делить и строить пространство в соответствии с этим законом. Во-первых, научитесь создавать прямоугольник идеальных пропорций. Используйте квадрат в качестве основы.
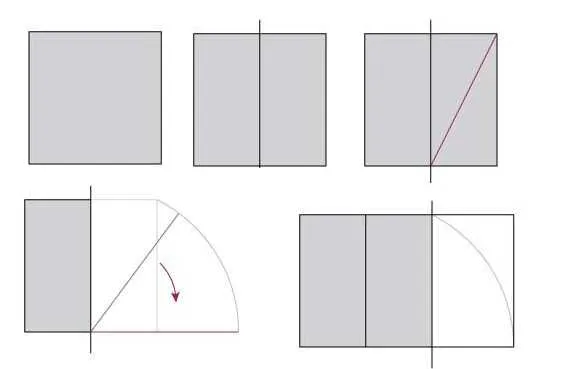
Прямоугольная структура золотого сечения
Квадрат делится пополам и проводится линия, соединяющая противоположные углы с одним из получившихся прямоугольников. Далее возьмите компас, поставьте иглу в центр нижней стороны квадрата, отложите длину получившейся диагонали и отметьте линию, которая будет продолжением нижней стороны квадрата. Равенство сторон полученного прямоугольника равно 1,62 (именно это равенство составляет 62% и 38%).
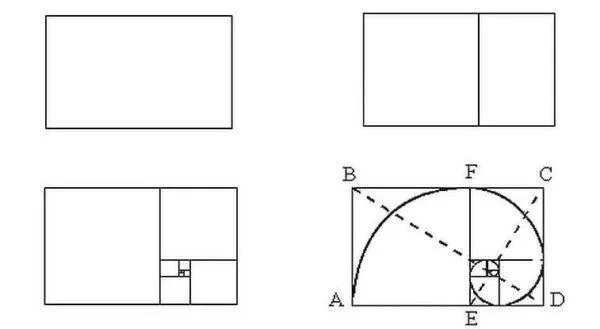
Это происходит по очевидным причинам. Однако не все следуют этой схеме.
Самое интересное, что если вы начнете делить прямоугольник с соотношением размеров 1,62 на квадрат и прямоугольник, вы снова создадите прямоугольник меньшего размера в идеальной пропорции. Если вы снова произведете деление по тому же принципу, то увидите еще одну пару квадратов и прямоугольников со сторонами, соотношение которых соответствует золотой пропорции. и так далее, до тех пор, пока возможно деление. Но еще интереснее то, что последовательность Фибоначчи, которая выглядит как разворачивающаяся спираль, идеально вписывается в это деление. Иллюстрация показана выше.
Как разделить отрезок по правилу золотого сечения
Эта функция полезна, например, для проектирования домов, квартир, апартаментов и мебели. Аналогично, он может потребоваться для оформления участков, клумб, посадок и т.д. В общем, его можно использовать практически везде.

В нем нет ничего особенного, но от него трудно оторвать взгляд. Знаете ли вы, почему;
Итак, вот как разделить отрезок, используя правило золотого сечения
- Берем отрезок, делим его пополам.
- Из одного из концов восстанавливаем перпендикуляр (прямая под углом 90°), который длиной равен половине отрезка. На рисунке это отрезок BC .
- Полученную точку C соединяем прямой с другим концом отрезка ( A ).
- На отрезке AC ставим точку D. Она находится на расстоянии, равном длине отрезка BС. Проще всего это сделать при помощи циркуля, но можно и линейкой.
- Замеряем длину отрезка AD (снова циркулем, либо линейкой). Такую же длину откладываем на отрезке AB. Получаем точку E .
- Теперь, если измерить длины отрезков AE и EB и разделить их, получим то самое заветное число — 1,62.
Узнайте, как повторить этот процесс несколько раз, и все это за несколько минут. Вы также можете использовать эти соотношения, если, например, вам нужно указать высоту или форму окна. Используя те же принципы, можно определить положение всех элементов здания и их размеры. При проектировании существующих предметов проще разделить их на проценты. Здесь вы уже считаете в уме или с помощью калькулятора.
Идеальный треугольник и пентаграмма
Идеальный вариант называется равнобедренным треугольником, основание которого равно 1/3 длины боковых сторон. Это означает, что здесь также наблюдается золотое сечение. Нарисовать треугольник с идеальным соотношением сторон несложно. Компас удобнее, но можно использовать и линейку.

Золотой треугольник, правила его построения и применение в оформлении интерьера.
Состав следующий. От точки A отложите любую длину прямой три раза. Обозначим через O. Получите точку B. Это позволяет провести линию, перпендикулярную AB. Ограничьте значение O этой линией по обе стороны от точки B. Найдены две точки d и d1. Соедините их с точкой А. Это создает треугольник со значением стороны 1,62. Это можно проверить, определив длину основания стороны (точка C) с помощью компаса. Вторая проверка заключается в том, что противоположный угол равен 36°.
Создание клёпки немного сложнее. Она регистрируется на круге и не может быть выполнена без компаса.
- Центр окружности обозначаем O , через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
- Находим середину отрезка OD , ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D .
- Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E , ведем грифель до пересечения с радиусом. Вот и получили точку C .
- Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.
Интересно, что если нарисовать звезду, используя вершины полученного става, то она будет состоять из полного треугольника.
После его открытия эти числа стали известны знаменитым математикам. Примечательность последовательности чисел Фибоначчи заключается в том, что каждое число в этой последовательности получается из суммы двух предыдущих чисел.
Последовательность Фибоначчи и золотое сечение
Около 1200 года математик Леонардо Фибоначчи обнаружил уникальное свойство последовательности Фибоначчи. Эта последовательность напрямую связана с золотым сечением, потому что когда вы получаете два последовательных числа Фибоначчи, их соотношение очень близко к золотому сечению. По мере увеличения числа коэффициент приближается к 1,618. Например, отношение 3 к 5 равно 1,666. Однако соотношение 13 к 21 составляет 1,625. Все чаще соотношение 144 к 233 составляет 1,618. Все эти числа являются последовательными числами в последовательности Фибоначчи.
Такие соотношения из последовательности Фибоначчи, которые близки к значению золотого сечения, можно применить к прямоугольному соотношению, называемому золотым прямоугольником. Она известна как одна из самых визуально совершенных геометрических форм. Поэтому правило золотого сечения широко используется во всех видах изобразительного искусства. Золотой прямоугольник также ассоциируется с золотой спиралью, которая создается путем построения соседних квадратов меры Фибоначчи.
Пропорции золотого сечения в материальном мире
В 1509 году Лука Пачоли написал книгу, в которой назвал число F «Божественной пропорцией». Это было проиллюстрировано ЛеонардодаВинчи. Позднее да Винчи назвал это соотношение золотым сечением. Он использовался для достижения баланса и красоты во многих картинах и скульптурах эпохи Возрождения.
Сам да Винчи использовал золотое сечение для определения всех пропорций «Тайной вечери», включая размеры стола, пропорции стен и детали интерьера. Золотое сечение также присутствует в картинах да Винчи «Витрувианский человек» и «Моннализа». Считается, что золотое сечение использовали и другие великие художники, такие как Михаил Ангелос, Рафаэль, Рембрандт, Серат и Сальвадор Дали.
Термин «фи» был введен американским математиком Марком Барром в 1900-х годах. Фи продолжали использовать в математике и физике, включая плитку Пенроуза в 1970-х годах для придания пятикратной симметрии мозаичным поверхностям. В 1980-х годах F появился в недавно открытой форме материи — квантовых кристаллах.
Phi — это не просто загадочный и непонятный термин в математике и физике. Он появляется вокруг нас в нашей повседневной жизни, даже в наших эстетических взглядах. Исследования показали, что когда испытуемые смотрят на случайные лица, более привлекательными оказываются те, которые имеют явное сходство с золотым сечением. Лица, оцененные как наиболее привлекательные, демонстрируют золотое соотношение ширины лица и ширины глаз, носа и бровей. Испытуемые не были математиками или физиками, знающими законы золотого сечения (обычные, среднестатистические люди), и это вызвало инстинктивную реакцию.
Золотое сечение также проявляется в природе и науке всех видов. Ниже приведены примеры того, где это бывает наиболее неожиданно.
- Цветочные лепестки. Количество лепестков на некоторых цветах соответствует последовательности Фибоначчи. С точки зрения теории Дарвина считается, что каждый лепесток помещается таким образом, чтобы обеспечить максимально возможное воздействие солнечного света и других факторов.
- Семенные головки. Семена цветка часто начинают произрастать в центре семенной головки и мигрируют наружу, заполняя свободное пространство. Например, семечки подсолнухов следуют этой схеме.
- Сосновые шишки. Семенные коробочки сосновых шишек наполнены семенами, которые растут спирально вверх, в противоположных направлениях. Количество шагов, которые делают спирали, как правило, соответствует числам Фибоначчи.
- Ветви дерева. То, как ветки дерева формируются или расщепляются, является примером последовательности Фибоначчи. Корневые системы и водоросли также придерживаются такого способа формирования.
- Раковины. Многие раковины, в том числе раковины улитки и раковины наутилуса, являются прекрасными примерами золотой спирали.
- Спиральные галактики. Млечный путь имеет несколько спиральных рукавов, каждый из которых имеет логарифмическую спираль примерно 12 градусов. Форма спирали идентична золотой спирали, а золотой прямоугольник можно нарисовать над любой спиральной галактикой.
- Ураганы. Внутреннее строение ураганов часто следует правилу золотой спирали.
- Пальцы руки человека. Каждый участок пальца от кончика основания до запястья больше, чем предыдущий, примерно на соотношение Ф.
- Тела человека и животных. Расстояние от пупка человека до пола и от макушки головы до пупка – это золотое сечение. Но человек не единственный пример золотого сечения в животном мире. Дельфины, морские звезды, морские ежи, муравьи и пчелы также демонстрируют эту пропорцию.
- Молекулы ДНК. Молекула ДНК имеет размеры 34 ангстрем на 21 ангстрем на каждом полном цикле спирали в виде сдвоенной спирали. В рядах Фибоначчи 34 и 21 являются последовательными числами.
Вот лишь несколько видов спиральных раковин с логарифмическим ростом по научному названию: Haliotis Parvus, Dolium Perdix, Murex, Fusus Antiquus, Scalari Pretiosa, SolariumTrochleare.
Золотая пропорция в строении легких человека
Американские физики Б.Д. Вест и доктор А.Л. Голдбергер, изучая физиогномику, обнаружили, что структура человеческого легкого также имеет золотое деление.
Бронхиолы, из которых состоят легкие человека, характеризуются своей асимметрией. Петля состоит из двух основных дыхательных путей, один из которых (левый) длиннее, а другой (правый) короче.
*Эта асимметрия сохраняется во всех петлях разветвления мелких дыхательных путей. Соотношение длин коротких и длинных петель также является золотым сечением — 1:1,618.
Строение золотого ортогонального четырехугольника и спирали
Золотая пропорция — это пропорциональное деление отрезка на неравные части так, что большая часть сама относится к меньшей, и поэтому весь отрезок относится к большей части. Другими словами, малая часть связана с большой частью. Он так же велик, как и все остальное.
В геометрии прямоугольник с таким соотношением сторон называется золотым прямоугольником. Его длинная сторона относится к короткой в соотношении 1,168:1.
Золотой прямоугольник также обладает многими замечательными свойствами. Золотой прямоугольник обладает многими необычными свойствами. Если из золотого прямоугольника вырезать квадрат, стороны которого равны меньшим сторонам прямоугольника, то снова получится золотой прямоугольник меньших размеров. Этот процесс может продолжаться бесконечно. Продолжая нарезать квадраты, можно получить все более мелкие золотые прямоугольники. Затем у них появляется логарифмическая спираль. Это важно для математических моделей физических объектов (например, раковины улитки).
Полюса спирали лежат на пересечении диагонали исходного прямоугольника и первого вертикального разреза. Кроме того, диагонали всех последующих нисходящих золотых прямоугольников лежат на этих диагоналях. Есть, конечно, и золотые треугольники.
Британский дизайнер и парикмахер Уильям Чарльтон утверждает, что спиралевидная форма приятна для глаз, и люди используют их на протяжении тысячелетий, объясняя это.
‘Мне нравится вид спирали, потому что ее легко изучить визуально’.
В природе
*Правило золотого сечения, определяющее структуру спирали, очень часто встречается в природе в творениях непревзойденной красоты. Наиболее очевидным примером является спиральная форма, наблюдаемая в расположении семян подсолнечника, сосновых шишек, ананасов, кактусов и лепестков роз.

* Ботаники обнаружили, что в расположении листьев на ветке, семян подсолнечника или сосновых шишек очевиден порядок Фибоначчи, а значит, и закон золотого сечения.
Всемогущий Бог дал каждому из своих творений особую меру и соразмерность. Это подтверждается примерами, найденными в природе. Существует множество примеров того, что процессы развития живых организмов строго следуют форме логарифма.
Все пружины в витках имеют одинаковую форму. Математики обнаружили, что форма витка остается неизменной при увеличении размера пружины. Ни одна другая форма математики не обладает такими уникальными свойствами, как спираль.