Это безумное доказательство является математически верным. Мы еще вернемся к этому, когда будем говорить о математической логике и о том, как она работает в жизни.
Реально сложные задачи
Если вам нравится ломать голову и вы любите сложные задачи, эта игра для вас. Каждый из них включает в себя относительно простую математику, а также умопомрачительную логику, которая оказывается верной. Если вы можете решить все эти проблемы самостоятельно, без наших советов, напишите об этом в комментариях, потому что ИТ-индустрия должна знать своих героев.
Одна бабушка решила заняться фермерством — выращивать помидоры и продавать их. Она собрала 100 килограммов помидоров, погрузила их в тележку и утром поставила возле дома.
Помидоры, которые выращивала ее бабушка, на 99% состоят из воды, но на солнце часть воды испаряется через кожицу. День был жарким, и к вечеру содержание воды в помидорах составило 98 %. Сколько сейчас весят бабушкины помидоры?
Результат может вас удивить, поэтому внимательно следите за расчетами.
Во-первых, давайте рассчитаем состав утренних помидоров. Они были на 99% заполнены водой. Это означает, что у них было 99 фунтов воды и 1 фунт клетчатки. Сегодня утром волокно составило 1%:
100% — 99% = 1%.
В зависимости от проблемы, этот килограмм волокна не может испариться или исчезнуть, его вес всегда остается неизменным. Испаряется только вода.
Теперь измерьте состав томата вечером: воды было уже 98%. Это означает, что количество воды уменьшилось, но все волокна остались на месте: Как утром был килограмм, так и сейчас. Но соотношение волокон и воды изменилось: теперь тот же килограмм волокон составляет 2% от общего веса. Итак, давайте подсчитаем, сколько весят все помидоры вечером:
2% помидоров весят 1 килограмм, значит 20% весят 10 килограмм.
Умножьте обе части на 5, чтобы получить общий вес. Мы получаем:
100% = 50 кг.
Оказалось, что к вечеру вес уменьшился вдвое! Это контринтуитивно, но именно так работает математика. ¯\_(ツ)_¯
Странный разговор двух программистов
Встречаются два программиста, которые давно не виделись. У них такой диалог:
— Я слышал, что у вас есть дети.
— Сколько им лет?
— Ну. Тринадцать по счету!
— Ты опять говоришь загадками? Хорошо. Что еще вы можете сказать?
— Если умножить возраст, то получится столько же, сколько окон вон в том доме.
Программист считает окна и рассчитывает варианты.
— Но даже этого недостаточно для ответа!
— Я хотел бы добавить, что мой старший сын — рыжий.
— Ну, это уже другой вопрос. Вы. (Ответ следует).
Сколько им было лет? И как первый мог угадать возраст?
Если вы все еще думаете, что эта проблема — полная ерунда, мы вас понимаем. И все же есть ясное, логичное и точное решение.
Его суть в том, что каждый ответ второго является уточнением или подсказкой к решению. А первый продолжал задавать вопросы, пока все подсказки не привели его к правильному ответу. Давайте проследим за ходом его мысли.
Первый ответ говорит нам о том, что всего детей трое. Хорошо, но явно недостаточно для вычисления возраста.
Второй ответ говорит нам
Третий ответ заключается в том, что произведение возрастов равно количеству окон. Кажется, что это бесполезно, потому что мы не знаем количество окон в доме — но это не так. Если бы этого ответа было достаточно, то первый ответ сразу бы указал на возраст, но поскольку это не так, то это означает, что информации недостаточно.
Давайте посмотрим на продукты всех возрастных комбинаций и попытаемся выяснить, что в них не так:
1 × 6 × 6 = 36
2 × 2 × 9 = 36
Поскольку этот ответ о количестве окон был недостаточным, в доме было так много окон, что было много результатов продуктов ниже этого числа. Мы перечислили их в таблице. Для всех остальных чисел был бы только один ответ о возрасте, а у числа 36 есть много вариантов, поэтому первый сказал, что этого недостаточно.
Четвертый ответ: старший сын — рыжий. Цвет волос для нас не так важен, как количество старших сыновей. Поскольку «старший сын» означает, что он самый старший, вариант 1 — 6 — 6 нам не подходит, так как старших сыновей двое. Это оставляет только один вариант: 2 — 2 — 9.
Ответ: Старшему сыну 9 лет, а двум другим по 2 года.
В 1990-х годах бандиты отвезли двух застройщиков на кладбище. Бандиты тайно выбрали 2 целых положительных числа, оба больше единицы, с суммой меньше 100. Первому программисту бандит сказал произведение этих чисел, а второму программисту — сумму чисел. Затем у программистов состоялся следующий разговор.
Странные программисты снова разговаривают
Первое: я понятия не имею, какая у вас сумма.
2: Хаха, для меня это не новость! Я уже знал, что ты этого не знаешь.
Первый: Ага! Теперь я знаю, сколько стоит ваша сумма!
Второй: Отлично — теперь я тоже знаю ваш продукт!
Грабители, конечно же, отпустили ее. Потому что это загадка! И загадка в том, что это за цифры и как программисты их получили.
В отличие от предыдущей задачи, здесь решение намного сложнее, так как для проверки чисел необходимо одновременно иметь в уме 2 или 3 условия. Но мы можем это сделать.
Чтобы решить ее, нам нужно вспомнить, что такое простые числа и какими особыми свойствами они обладают. Простое число — это число, которое делится только на себя и на единицу. Например, число 5 является простым числом, потому что оно делится только на 5 и на 1. Число 6 не является простым числом, потому что оно делится не только на 6 и 1, но и на 2 и 3 без остатка. Семь также является простым числом, но восемь — нет, потому что оно делится не только на 8 и 1, но и на 2 и 4.
Если вы перемножите два простых числа, вы не сможете получить результирующее произведение никаким другим способом (кроме умножения того же числа на единицу). Давайте объясним это.
Во-первых, я установил, что одно из чисел определенно не является простым числом, потому что в противном случае я бы сразу сделал его произведением двух простых чисел и легко нашел бы сумму. А если это так, то одно из чисел m или n может быть получено путем умножения двух других чисел. Таким образом, общий продукт состоит как минимум из трех множителей, и как минимум один из них отличается от остальных — поэтому существует множество возможных сумм, и я не знаю, какая из них правильная (запомните это как правило 1).
Во-вторых, сумма, которую я имею, не может быть получена из двух простых чисел, поэтому ваше произведение также не может быть разложено на два простых фактора. Это означает, что у меня нечетная сумма, поскольку, согласно гипотезе Гольдбаха, в нашем случае мы можем получить любое четное число путем сложения двух простых. А поскольку двух простых чисел не существует, сумма нечетна. А еще эта сумма определенно не равна сумме двух и простого числа, потому что два — тоже простое число, ха! Итак, существует несколько вариантов суммы m и n, удовлетворяющих вашим условиям, но я пока не могу определить, какие именно (запишем их как Правило 2).
Во-первых, из всех множителей в моем продукте я могу составить только пару вариантов, сумма которых удовлетворяет вашему ограничению — она не распадется на сумму двух простых или сумму чисел множителя (правило 3).
Другие названия: гипотеза 3n+1, сиракузская проблема, сеть чисел. Если взять любое натуральное число n и выполнить с ним следующие преобразования, то рано или поздно всегда получится единица. Четное n нужно разделить на два, а нечетное n нужно умножить на 3 и прибавить единицу. Для числа 3 последовательность будет такой: 3×3+1=10, 10:2=5, 5×3+1=16, 16:2=8, 8:2=4, 4:2=2, 2:2=1. Конечно, если продолжить преобразования от единицы, то начнется цикл 1,4,2. Очень быстро количество вычислительных шагов начинает превышать сотню, и каждая новая последовательность требует все больше ресурсов для решения.
Еще в прошлом месяце в решении этой почти столетней проблемы был достигнут незначительный прогресс. Но знаменитый американский математик Терренс Тао ближе всех подошел к разгадке головоломки, и он до сих пор не нашел ответа. Догадка Коллатца лежит в основе такой математической дисциплины, как динамические системы, которая, в свою очередь, имеет отношение к ряду других прикладных наук, таких как химия и биология. Проблема Сиракуз выглядит как простой, невинный вопрос, но именно это и делает ее такой особенной. Почему ее так трудно решить?
Еще одна проблема, формулировка которой кажется простой: любое четное число (больше 2) можно представить в виде суммы двух простых чисел. Это краеугольный камень современной математики. Это утверждение можно легко проверить.
Эта проблема была сформулирована Христианом Гольдбахом в его переписке с Леонардом Ойлером, другим великим представителем математики, в 1742 году. Сам Кристиан сформулировал вопрос несколько проще: «Каждое нечетное число больше 5 может быть представлено в виде суммы трех простых чисел». В 2013 году перуанский математик Харальд Хельфготт нашел окончательное решение этой проблемы. Однако следствие из этого утверждения, предложенного Эйлером, известное как бинарная проблема Гольдбаха, до сих пор никому не было известно.
Числа-близнецы называются простыми числами, которые отличаются только на 2. Например, 11 и 13, или 5 и 3, или 599 и 601. Если бесконечность простых чисел была доказана многократно с древности, то бесконечность чисел-близнецов находится под вопросом. Начиная с 2, между первичными числами нет четных чисел, а начиная с 3, нет чисел, кратных трем. Следовательно, количество возможных близнецов становится все меньше и меньше, если убрать из серии все те, которые отвечают «правилам деления». Единственным модулем для формулы нахождения таких чисел является 6, и формула выглядит следующим образом: 6n±1.
Гипотеза Коллатца
Как всегда в математике, когда проблема не решается «с головы», к ней подходят с другой стороны. В 2013 году, например, было доказано, что количество простых чисел, отличающихся на 70 миллионов, бесконечно. Менее чем через месяц значение разности увеличилось до 59 470 640, а затем на порядок — до 4 982 086. Существуют теоретические обоснования бесконечных пар простых чисел с разностью 12 и 6, но доказана только разность 246. Как и другие проблемы такого рода, гипотеза близнецовых чисел имеет особое значение для криптографии.
Догадка Ходжа была сформулирована в 1941 году и заключается в том, что для особенно хороших типов пространства, так называемых проективных алгебраических многообразий, так называемые круги Ходжа являются комбинациями геометрически интерпретируемых объектов — алгебраических кругов.
Проблема Гольдбаха (бинарная)
Упрощенно, можно сказать, что в 20 веке были открыты очень сложные геометрические формы, такие как изогнутые бутылки. Поэтому было предложено, что для построения этих объектов описания необходимо применять очень сложные формы, не имеющие геометрического содержания, «как ужасное многомерное пятно и клякса», либо можно обойтись обычной стандартной алгеброй + геометрией.
Здесь довольно трудно объяснить на человеческом языке, пока мы знаем, что решение этой проблемы будет иметь далеко идущие последствия в области распределения простых чисел. Проблема настолько важна и актуальна, что даже выведение контрпримера к гипотезе отдано на усмотрение совета университета, проблему можно считать доказанной, поэтому здесь можно попробовать и обратный метод
Гипотеза о числах-близнецах
Говард Воловиц, конечно, помог бы нам здесь, если бы он действительно существовал — в конце концов, это гидродинамическая загадка, причем фундаментальная. Уравнения описывают движения вязкой ньютоновской жидкости, имеют большое практическое значение и, прежде всего, описывают турбулентность, которая не поддается научному контролю и свойства и эффекты которой никогда не могут быть предсказаны. Логика этих уравнений позволит нам не тыкать пальцем в небо, а понять турбулентность изнутри и сделать самолеты и механизмы более устойчивыми.
Гипотеза Римана — самая известная и бесспорная нерешенная математическая проблема. За решение головоломки полагается большая награда
Гипотеза Ходжа
Короче говоря, Бернхард Риман предположил, что распределение простых чисел в множестве всех натуральных чисел не подчиняется никакому закону. Однако их количество на определенном участке числовой прямой коррелирует с распределением определенных значений на графике дзета-функции. Она находится выше и дает бесконечное число членов для каждого s. Например, если s заменить на 2, то получится уже решенная «базельская задача» — серия обратных квадратов (1 + 1/4 + 1/9 + 1/16 + …). Одна из «проблем тысячелетия», за решение которой предлагается приз в миллион долларов, а также включение в пантеон «богов» современной математики. На самом деле, доказательство этой гипотезы продвинет теорию чисел настолько, что это событие по праву можно будет назвать историческим. Многие вычисления и утверждения в математике основаны на предположении, что «гипотеза Римана» верна, и до сих пор она никого не разочаровала. Немецкий математик сформулировал знаменитую проблему 160 лет назад, и с тех пор ее решали бесчисленное количество раз, но она по-прежнему остается, пожалуй, самой неразрешимой проблемой в современной математике.
Еще одна «проблема тысячелетия», на решение которой Институт Клэя выделит миллион долларов. Для не-математика довольно сложно сформулировать и понять суть гипотезы, хотя бы в общих чертах. Бирч и Свиннертон-Дайер начали с определенных свойств эллиптических кривых. Идея заключалась в том, что порядок кривой можно определить, зная нулевой порядок дзета-функции. Как говорится, ничего не ясно, но очень интересно. Эллиптические кривые — это линии на графике, описываемые безобидными на первый взгляд уравнениями вида y²=x³+ax+b. Некоторые из их свойств чрезвычайно важны для алгебры и теории чисел, и решение этой проблемы может значительно продвинуть науку. Наибольший прогресс в решении этой нерешенной математической проблемы был сделан в 1977 году группой математиков из Англии и США.

Гипотеза Римана
Это не просто одна проблема, а целая категория проблем. И мы сталкиваемся с ними каждый день, например, когда хотим расположить фрукты на холодильной полке или когда хотим как можно более плотно расставить бутылки на полке. Математически мы должны определить среднее количество контактов («поцелуев», также называемых числом контактов) отдельных шаров с другими. На сегодняшний день существуют точные решения для размерностей 1-4 и 8. Размерность или размерность означает количество линий, вдоль которых расположены шарики. В реальной жизни существует только третье измерение, но математика работает и с гипотетическими величинами. Решение этой проблемы может не только серьезно продвинуть теорию чисел и геометрию, но и помочь в химии, информатике и физике. Возможно, это одна из немногих нерешенных математических задач, которые имеют четкие практические приложения.
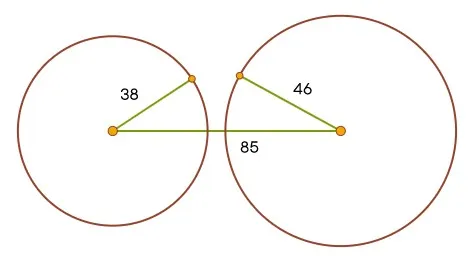
Такого треугольника не существует. Длины сторон не соответствуют теореме о неравенстве треугольника, которая гласит, что сумма любых двух сторон должна быть больше третьей. Это можно доказать геометрически: Возьмите отрезок длиной 85 и нарисуйте на его концах окружности с радиусами 38 и 46. Эти окружности не пересекаются, поэтому найти третью вершину треугольника невозможно.

Уравнения Навье-Стокса
Будет интересно применить формулу Герона для вычисления площади этого не треугольника. Из этого возникнут интересные вопросы!

Гипотеза Римана
Существует несколько способов определить невозможность такого полинома. Например, эти условия нарушают теорему о рациональных корнях, которая гласит, что любой рациональный корень многочлена должен быть отношением делителя свободного члена (d) к делителю первого множителя (2).
Наш любопытный факт о полных квадратах доказывает, что эта проблема невозможна. Единицы полного квадрата могут содержать только цифры 0, 1, 4, 5, 6 или 9. Это можно доказать, возведя в квадрат все возможные цифры и наблюдая за возможными результатами. Поскольку ни один полный квадрат не может заканчиваться цифрами 2, 3, 7 или 8, не существует полного квадрата, состоящего только из этих цифр.
Гипотеза Берча и Суиннертон-Дайера
Какой бы ни была ваша проблема, всегда полезно иметь доступные и надежные серверы. Даже для сложных математических расчетов максимальная конфигурация — 128 ядер CPU, 512 ГБ RAM, 4000 ГБ NVMe.
Проблема плотной упаковки равных сфер