Впервые этот термин был упомянут К. А. Браунли в его трудах в 1960 году. Он описал p-значение значимости как показатель, который находится в обратной зависимости от правдивости результатов. Чем выше p-значение, тем ниже уверенность выборки в связи между переменными.
Статистическая значимость в экспериментах и анализе данных
Добро пожаловать в 11-ю часть нашей серии статей о статистике в электротехнике. До сих пор мы обсуждали как общие определения, так и конкретные примеры статистических концепций, полезных для инженера-практика. Если вы хотите узнать больше о темах, которые мы рассмотрели, пожалуйста, прочитайте статьи, перечисленные в оглавлении выше.
Каждый, кто регулярно читает научные статьи, часто сталкивается со «статистической значимостью», часто сопровождаемой загадочной ссылкой на p
Статистическая значимость — это важный инструмент, который помогает исследователям понять, что на самом деле показали их эксперименты и данные, и помогает коллегам решить, заслуживают ли представленные результаты дальнейшего рассмотрения или исследования.
В то же время, статистическая значимость — это несколько расплывчатое понятие, которое легко может быть неверно истолковано и вызвало много споров в научном сообществе.
Не так давно три профессора опубликовали в журнале Nature «аннотированную» статью, в которой рекомендовали полностью отказаться от статистической значимости как основы для принятия или отклонения гипотезы — и им понадобилась всего неделя, чтобы найти еще 800 ученых и исследователей, готовых официально согласиться с их точкой зрения.
Что такое статистическая значимость?
Эксперимент начинается с нулевой гипотезы, которая утверждает, что между двумя явлениями, по которым собираются данные, нет взаимосвязи. Если цель эксперимента — найти или доказать какую-то связь или влияние, нулевая гипотеза эквивалентна утверждению, что эксперимент «провалился».
Статистическая значимость — это математический критерий, с помощью которого мы можем решить, принять или отвергнуть нулевую гипотезу.
Статистически значимый результат, основанный на заранее определенном пороге вероятности, указывает на то, что мы должны отвергнуть нулевую гипотезу; другими словами, что-то произошло (наблюдалась связь, был получен эффект, связь существует), и поэтому эксперимент дал что-то потенциально значимое или интересное.
Явления, которые контролируются случайными процессами, обычно приводят к нормальному распределению значений. Поэтому концептуальную нулевую гипотезу принято представлять в виде гауссовой кривой, то есть распределения наблюдений, которое можно было бы ожидать, если бы одна экспериментальная переменная была независима от другой экспериментальной переменной.
Порог вероятности
Сайт
Если p-значение достаточно низкое, то нет причин продолжать считать, что между двумя переменными нет связи. Таким образом, мы отвергаем нулевую гипотезу и утверждаем, что связь существует.<0,05) или 1% ( p<0,01) или какой-либо другого порога (p<⍺, где ⍺ обозначает требуемый уровень значимости ).
P-значение — это значение, используемое при проверке статистических гипотез. Это вероятность ошибки, когда нулевая гипотеза отвергается (первый тип ошибки). Проверка гипотез с помощью P-значения является альтернативой классической проверке с использованием критического значения распределения.
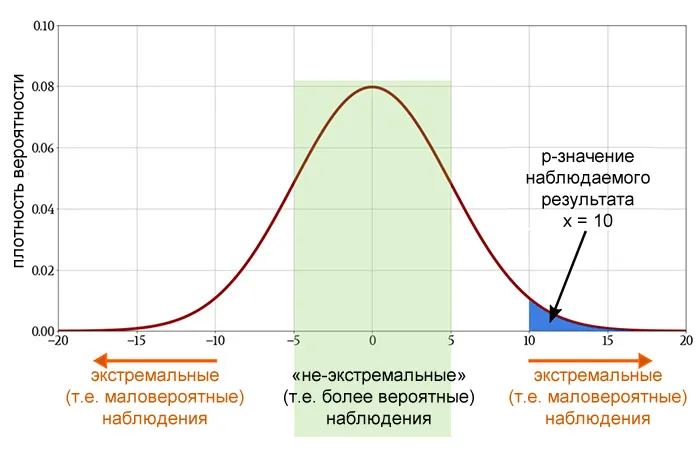
В общем случае P-значение равно вероятности того, что случайная величина с заданным распределением (распределение статистического теста при нулевой гипотезе) будет иметь значение, которое не меньше истинного значения статистического теста. Википедия.
p-значение
Другими словами, p-значение — это наименьшее значение уровня значимости (т.е. вероятности отвергнуть справедливую гипотезу), для которого рассчитанная контрольная статистика приводит к отвержению нулевой гипотезы. Обычно p-значение сравнивают с обычными стандартными уровнями значимости 0,005 или 0,01.
Например, если p-значение, рассчитанное по выборке, равно p = 0,005, это означает вероятность 0,5% для проверки гипотезы. Чем меньше p-значение, тем лучше, так как это увеличивает «силу» отклонения нулевой гипотезы и повышает ожидаемую значимость результата.
На Хабре этому есть интересное объяснение.
Статистический анализ похож на черный ящик: на входе — данные, на выходе — таблица с основными результатами и значением значимости (p-value).
Допустим, мы хотим выяснить, существует ли корреляция между зависимостью от кровавых компьютерных игр и агрессией в реальной жизни. Для этого мы случайным образом сформировали две группы по 100 студентов в каждой (группа 1 — любители стрелялок, группа 2 — не играющие в компьютерные игры). Количество драк со сверстниками, например, служило индикатором агрессивности. Наше фиктивное исследование показывает, что у группы студентов, которые играют в игры, действительно значительно чаще возникают конфликты со сверстниками. Но как определить, являются ли эти различия статистически значимыми? Является ли наблюдаемое различие чисто случайным? Чтобы ответить на эти вопросы, мы используем р-значение значимости (p-value), то есть вероятность того, что такие или более выраженные различия существуют, когда на самом деле в популяции различий нет. Другими словами, это вероятность того, что существуют такие или даже более выраженные различия между нашими группами, если предположить, что компьютерные игры на самом деле не оказывают никакого влияния на агрессию. Это звучит не слишком сложно. Однако эта конкретная статистика слишком часто интерпретируется неправильно.
Мы
О чём говорит p-value?
1. вероятность того, что компьютерные игры являются причиной агрессивного поведения, составляет 96%; 2. вероятность того, что агрессия и компьютерные игры не связаны, составляет 0,04; 3. p-значение, превышающее 0,05, означает, что агрессия и компьютерные игры вообще не связаны. 4. вероятность случайного возникновения таких различий равна 0,04. 5. все утверждения ложны.

Если вы выбрали пятый вариант, то вы абсолютно правы! Но, как показывают многочисленные исследования, даже люди с большим опытом анализа данных часто неправильно интерпретируют p-значение.
Давайте рассмотрим ответы по очереди:
Первое утверждение является примером ошибки корреляции: тот факт, что две переменные значительно коррелируют, ничего не говорит о причине и следствии. Возможно, именно более агрессивные люди предпочитают проводить время за компьютерными играми, а не компьютерные игры делают людей более агрессивными.
Это более интересное заявление. Дело в том, что сначала мы предполагаем, что различий нет. Исходя из этого, мы вычисляем p-значение. Поэтому правильная интерпретация следующая: «Если предположить, что агрессия и компьютерные игры никак не связаны, то вероятность того, что такие или более выраженные различия существуют, составила 0,04.
Но что, если у нас лишь незначительные различия? Означает ли это, что между рассматриваемыми переменными нет взаимосвязи? Нет, это просто означает, что различия могут быть, но мы не смогли обнаружить их в наших результатах.
1 Определите ожидаемые результаты вашего эксперимента
Когда ученые проводят эксперимент, они обычно уже имеют представление о том, что они считают «нормальными» или «типичными» результатами. Это может быть основано на экспериментальных результатах предыдущих испытаний, достоверных наборах данных, данных из научной литературы или какого-либо другого источника. Определите ожидаемые результаты вашего эксперимента и выразите их в цифрах.
Как найти p-value?
Пример: Например, предыдущие исследования показали, что в вашей стране красные автомобили штрафуют чаще, чем синие. Например, среднее значение результатов показывает, что предпочтение красных автомобилей перед синими составляет 2:1. Мы хотим выяснить, имеет ли полиция в вашем городе такое же предвзятое отношение к цвету автомобилей. Для этого мы проанализируем штрафы за превышение скорости. Если мы возьмем случайный набор из 150 штрафов за превышение скорости, выписанных на красные или синие автомобили, мы ожидаем, что 100 штрафов будут выписаны на красные автомобили и 50 — на синие, если полиция в нашем городе так же предвзято относится к цвету, как и в стране.
Определите наблюдаемые результаты вашего эксперимента
Теперь, когда вы определили ожидаемые результаты, вам необходимо провести эксперимент и определить фактические (или «наблюдаемые») значения. Опять же, вам нужно представить эти результаты в цифрах. Если мы создадим экспериментальные условия и
Пример: Например, в нашем городе мы случайным образом выбрали 150 штрафов за превышение скорости, выписанных на красные или синие автомобили. Мы обнаружили, что 90 штрафов было выписано на красные автомобили и 60 — на синие. Это отличается от ожидаемых результатов в 100 и 50 соответственно. Действительно ли наш эксперимент (в данном случае изменение источника данных с национального на городской) вызвал такое изменение результатов, или полиция в нашем городе так же необъективна, как и в среднем по стране, и мы просто наблюдаем случайную вариацию? P-значение поможет нам определить это.
3. определите число степеней свободы в вашем эксперименте.
Число степеней свободы — это степень изменчивости в вашем эксперименте, определяемая количеством тестируемых категорий. Уравнение для числа степеней свободы таково: число степеней свободы = n-1, где «n» — число категорий или переменных, которые вы анализируете в своем эксперименте.
Пример: В нашем эксперименте есть две категории исходов: одна категория для красных автомобилей и одна категория для синих автомобилей. Поэтому в нашем эксперименте мы имеем 2-1 = 1 степень свободы. Если бы мы сравнивали красные, синие и зеленые автомобили, у нас было бы 2 степени свободы, и так далее.
4. сравнить ожидаемые и наблюдаемые результаты с помощью теста хи-квадрат.
Хи-квадрат (пишется «x2») — это числовое значение, которое измеряет разницу между ожидаемыми и наблюдаемыми значениями эксперимента. Уравнение для хи-квадрат имеет вид x2 = S((o-e)2/e), где «o» — наблюдаемое значение, а «e» — ожидаемое значение. Сложите результаты этого уравнения для всех возможных исходов (см. ниже).
Как мы уже выяснили, p — это вероятность. Это означает, что это действительное число от 0 до 1. Если контрольная статистика — это один из способов измерения того, насколько экстремальной является статистика для конкретной выборки, то p-значения — это другой способ измерения.
При сборе выборочной статистики всегда следует задавать вопрос: «Является ли эта выборка случайной, если верна только нулевая гипотеза?», или нулевая гипотеза ложна? «Если p-значение мало, это может означать одно из двух:
Интерпретация P-значение
В общем, чем меньше p-значение, тем больше у нас доказательств против нулевой гипотезы.
Насколько малым должно быть p-значение, чтобы отвергнуть нулевую гипотезу? Ответ на этот вопрос таков: «Это зависит от ситуации». Как правило, p-значение должно быть меньше или равно 0,05, но это значение не является универсальным.
- Нулевая гипотеза верна, но мы просто Мне очень повезло с получением нашей наблюдаемой выборки.
- Наша выборка такова, потому что нулевая гипотеза ложна.
Перед проверкой гипотезы мы обычно выбираем пороговое значение. Если p-значение меньше или равно этому порогу, нулевая гипотеза отвергается. В противном случае мы можем отвергнуть ню
Насколько мало – значит мало Достаточно?
Нулевая гипотеза — базовое условие, при котором нет разницы между текущей и новой версией целевой страницы с точки зрения конверсии.
Альтернативная гипотеза — предполагает, что изменение цвета кнопки на странице приводит к увеличению конверсии.
Проверка статистических гипотез
Рандомизация и нормализация нулевой гипотезы проводится в статистике.
Рандомизация нулевой гипотезы — наблюдаемый нами шаблон пространственных данных является одной из многих вариаций организации пространственных данных. Все остальные вариации не будут значительно отличаться от наблюдаемых.

Нормализация нулевой гипотезы подразумевает, что наблюдаемые значения являются одним из многих случайно выбранных вариантов. Ни пространственное расположение данных, ни их значения не определены.
p-значение позволяет нам увидеть, насколько правдоподобна нулевая гипотеза на основе данных выборки. Таким образом, если нулевая гипотеза подтвердится, p-значение указывает на отсутствие увеличения коэффициента конверсии в результате изменения цвета кнопки.
p-значение можно использовать для выявления доказательств, отвергающих нулевую гипотезу (базовую гипотезу) в ходе эксперимента.
Мы уже упоминали, что уровень значимости задается до начала исследования, чтобы определить, насколько малым должно быть p-значение, чтобы отвергнуть нулевую гипотезу. Однако разные люди могут использовать разные уровни значимости в разных ситуациях, поэтому могут возникнуть трудности, когда другие люди интерпретируют результаты двух разных тестов. p-значение помогает решить эту проблему.
Рассмотрим пример, когда компания провела исследование, сравнивающее доходность двух активов. Тест и анализ проводили два человека, которые использовали одни и те же исходные данные, но применяли разные уровни значимости. Существует вероятность того, что эти люди сделают противоположные выводы о разнице между активами. Предположим, что один эксперт получил 90% доверительный уровень для отклонения нулевой гипотезы, а другой — 95% доверительный уровень. Среднее p-значение наблюдаемой разницы между результатами составило 0,08, что соответствует уровню доверия 92 %. В этом случае первый эксперт обнаружил бы значительную разницу между двумя доходами, в то время как второй эксперт не обнаружил бы статистически значимой разницы.
Чтобы избежать этого, можно указать p-значение эксперимента и позволить независимым наблюдателям самостоятельно оценить статистическую значимость итоговых данных. Такой подход к проверке утверждений получил название «подход p-value».
Подход p-value к проверке гипотез
Обычно p-значения определяются с помощью таблиц p-значений или специального статистического программного обеспечения. An R
Ручной расчет p осложняется обычными распределениями вероятности, характерными для проверки гипотез. Удобнее использовать статистическую таблицу или компьютер для расчета приблизительных значений cdf.
Обычно в начале исследования уже есть представление о том, какие цифры можно считать приемлемыми. Выводы могут быть основаны на опыте предыдущих испытаний, на достоверных наборах данных или на общей информации из научной литературы и других источников.
Опыт работы с целевыми страницами показывает, что целевые страницы с кнопкой CTA на первом экране привлекают примерно в два раза больше клиентов, чем версии без таких кнопок. Нам необходимо определить, действительно ли наличие кнопки влияет на посетителей сайта. Для этого мы будем анализировать конверсию в покупку. Если мы возьмем условные 300 конверсий, то предположим, что 200 из них приходятся на сайты с кнопками CTA, а 100 — на сайты без кнопки, предполагая, что пользователи предвидят наличие кнопки.
Как рассчитать P-value
Теперь нам нужно провести тест и получить реальные, т.е. наблюдаемые, значения, которые также выражаются в числовой форме. В условиях эксперимента, если фактические числа не совпадают с ожидаемыми, есть две возможности — либо это связано с действиями эксперимента, либо это произошло случайно. В данном случае цель определения p-значения — понять, действительно ли наблюдаемые значения настолько отличаются от ожидаемых, что нулевая гипотеза не отвергается.
Предположим, мы выберем 300 случайных конверсий с наших сайтов, которые либо имели кнопку на первом экране, либо не имели. Мы обнаружили, что 220 конверсий было совершено на сайтах с кнопкой, а 80 — на сайтах без нее. Результаты отличаются от ожидаемых 200 и 100 соответственно. Теперь нам нужно определить, действительно ли наш тест (добавление кнопки на первый экран) вызвал изменение значений или это была случайная вариация. Определить это помогает p-значение.
Как рассчитать p-значение, используя тестовую статистику
Число степеней свободы показывает, насколько сильно может измениться эксперимент. Степень изменчивости зависит от количества тестируемых категорий.
Значение p-value тесно связано с уровнем статистической значимости. Последнее также определяет результат эксперимента.
Отклонение нулевой гипотезы означает, что между проверяемыми переменными существует устойчивая связь.
Двусторонний эксперимент: P-value = 2 × мин>
Теперь, когда мы собрали некоторые выборочные данные о времени доставки, мы провели расчеты и выяснили, что среднее время доставки на 10 минут больше, с p-We
Пошаговый алгоритм расчета p-значения
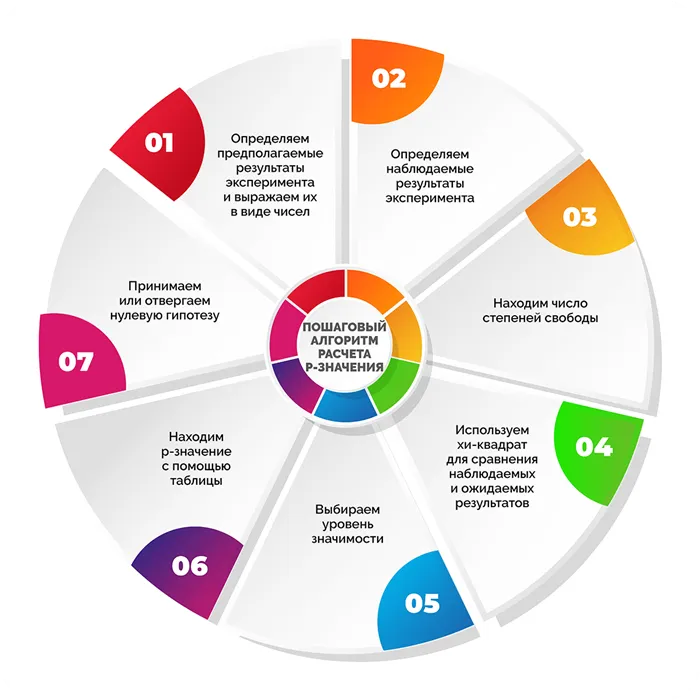
Шаг 1. Определяем предполагаемые результаты эксперимента и выражаем их в виде чисел
На мой взгляд, p-значения используются как инструмент, позволяющий опровергнуть наше первоначальное убеждение (нулевую гипотезу), когда результат статистически значим. В тот момент, когда мы чувствуем нелепость собственного убеждения (предполагая, что p-значение указывает на то, что результат статистически значим), мы отбрасываем свое первоначальное убеждение (отвергаем нулевую гипотезу) и принимаем логическое решение.
На этом последнем этапе мы складываем все вместе и проверяем, является ли результат статистически значимым.
Шаг 2. Определяем наблюдаемые результаты эксперимента
Недостаточно просто иметь p-значение, необходимо также установить порог (уровень значимости — альфа). Альфа всегда должна быть установлена до начала эксперимента, чтобы избежать предвзятости. Если наблюдаемое p-значение ниже альфы, результат является статистически значимым.
Как правило, значение альфа должно быть установлено на уровне 0,05 или 0,01 (опять же, значение зависит от вашей цели).
Шаг 3. Находим число степеней свободы
Как упоминалось ранее, результат является статистически значимым, если предположить, что перед началом эксперимента мы установили альфа на 0,05, поскольку p-значение 0,03 меньше альфа.
Как интерпретировать P-значение
Ниже описаны основные этапы всего эксперимента:
- Если p-значение меньше уровня значимости, то нулевую гипотезу можно смело отклонить и считать истинной альтернативную гипотезу.
- Если p-значение больше уровня значимости, это означает, что в ходе эксперимента выявили недостаточно оснований для отклонения нулевой гипотезы.
Если вы хотите узнать больше о статистической значимости, вы можете прочитать эту статью Уилла Керсена: Объяснение статистической значимости.
- вероятность того, что в ходе исследования наблюдения были случайными. То есть, если p = 0,05, есть 5% вероятности того, что наблюдаемое явление случайно и 95% вероятности того, что результат является следствием созданных условий;
- вероятность того, что будет сделан неверный вывод о взаимосвязи переменных. Если р = 0,05, то на каждые 100 экспериментов, где наблюдалась взаимосвязь, 95 их них действительно была, а 5 – нет.
P-значение в расчете времени доставки пиццы
Здесь есть что переварить, не так ли?
Я не могу отрицать, что p-значения смущают многих людей, и мне понадобилось некоторое время, чтобы действительно понять и оценить значение p-значений и то, как они могут быть применены в нашем процессе принятия решений в качестве специалистов по исследованию данных.
Однако не стоит слишком полагаться на p-значения, поскольку они помогают лишь в небольшой части всего процесса принятия решений.
Я надеюсь, что мое объяснение p-значений было интуитивно понятным и помогло понять, что на самом деле означают p-значения и как их можно использовать при проверке гипотез.
Вычислить p-значения очень просто. Это становится сложным, когда мы хотим интерпретировать p-значения при проверке гипотез. Надеюсь, теперь вам будет немного легче.
Если вы хотите узнать больше о статистике, я рекомендую эту книгу (которую я читаю прямо сейчас!) — Practical Statistics for Data Scientists, написанную специально для data scientist’ов, чтобы понять основные концепции статистики.
Узнайте больше о том, как вы можете освоить востребованную профессию с нуля или повысить свой уровень квалификации и зарплату, пройдя платные онлайн-курсы SkillFactory:
- Представьте, что мы живем в мире, где среднее время доставки всегда составляет 30 минут или меньше — потому что мы верим в пиццерию (наше первоначальное убеждение)!
- После анализа времени доставки собранных образцов р-значение на 0,03 ниже, чем уровень значимости 0,05 (предположим, что мы установили это значение перед нашим экспериментом), и мы можем сказать, что результат является статистически значимым.
- Поскольку мы всегда верили пиццерии, что она может выполнить свое обещание доставить пиццу за 30 минут или меньше, нам теперь нужно подумать, имеет ли это убеждение смысл, поскольку результат говорит нам о том, что пиццерия не выполняет свое обещание и результат является статистически значимым.
- Так что же нам делать? Сначала мы пытаемся придумать любой возможный способ сделать наше первоначальное убеждение (нулевая гипотеза) верным. Но поскольку пиццерия постепенно получает плохие отзывы от других людей и часто приводит плохие оправдания, которые привели к задержке доставки, даже мы сами чувствуем себя нелепо, чтобы оправдать пиццерию, и, следовательно, мы решаем отвергнуть нулевую гипотезу.
- Наконец, следующее разумное решение — не покупать больше пиццы в этом месте.
Статистическая значимость

- Сформулируйте нулевую гипотезу
- Сформулируйте альтернативную гипотезу
- Определите значение альфа для использования
- Найдите Z-показатель, связанный с вашим альфа-уровнем
- Найдите тестовую статистику, используя эту формулу
- Если значение тестовой статистики меньше Z-показателя альфа-уровня (или p-значение меньше альфа-значения), отклоните нулевую гипотезу. В противном случае не отвергайте нулевую гипотезу.
Последующие размышления
- Обучение профессии Data Science с нуля (12 месяцев)
- Профессия аналитика с любым стартовым уровнем (9 месяцев)
- Курс по Machine Learning (12 недель)
- Курс «Python для веб-разработки» (9 месяцев)
- Курс по DevOps (12 месяцев)
- Профессия Веб-разработчик (8 месяцев)