Доверительный интервал — это рассчитанный на основе выборки интервал значений характеристики, в котором с известной вероятностью содержится оцениваемый параметр популяции.
Доверительный интервал
Доверительный интервал — это предельное значение статистической величины, которое будет лежать в пределах этого интервала с заданной доверительной вероятностью γ при большем объеме выборки. Она обозначается как P(θ — e γ при значениях γ = 0,9, γ = 0,95, γ = 0,99, достаточно близких к единице.
- Доверительный интервал для общего среднего значения, доверительный интервал для дисперсии,
- доверительный интервал для стандартного отклонения, доверительный интервал для доли населения,
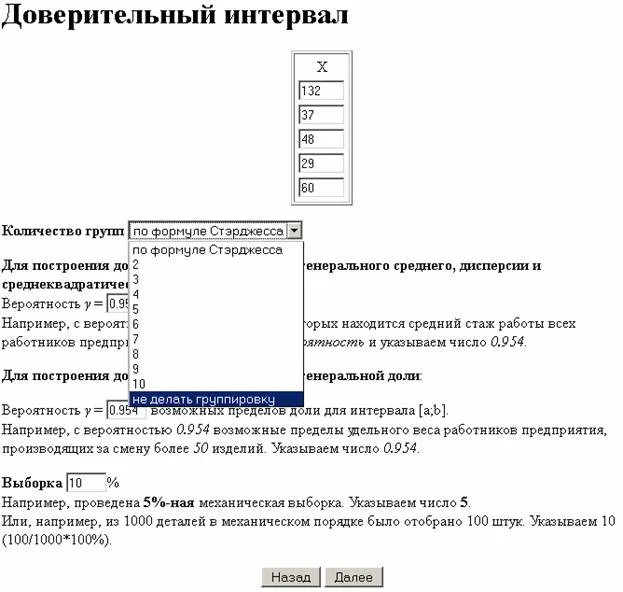
Если вы хотите найти доверительный интервал для набора переменных, воспользуйтесь этим калькулятором. Перед началом расчета может потребоваться сгруппировать данные. Также можно найти интервальное предсказание.
Пример 1. В колхозе 100 овец из общего стада в 1000 овец были подвергнуты выборочной контрольной стрижке. В результате средняя длина шерсти составила 4,2 кг на овцу. Определите с вероятностью 0,99 среднюю квадратическую ошибку выборки при определении средней стрижки одной овцы и пределов стрижки, когда дисперсия равна 2,5. Отбор проб должен быть повторен. Пример 2: 20 образцов продукта А были отобраны случайным образом из партии импортных продуктов на Северной таможне в Москве. Проверка показала, что среднее содержание влаги в образце продукта «А» составляет 6 % при среднеквадратичном отклонении 1 %. Определите с вероятностью 0,683 пределы для среднего содержания влаги в продукте во всей партии импортированного продукта. Пример 3: Опрос 36 студентов показал, что среднее количество книг, прочитанных за учебный год, составило 6. Предполагая, что количество книг, прочитанных студентом за семестр, имеет нормальное распределение со стандартным отклонением 6, найдите: A) пространственную оценку математического ожидания этой случайной величины с надежностью 0,99; B) какова вероятность того, что среднее количество текстов, прочитанных студентом за семестр, вычисленное по выборке, отклоняется от математического ожидания на абсолютную величину не более 2.
Классификация доверительных интервалов
По виду оцениваемого параметра:
По типу выборки:
- Доверительный интервал для бесконечной выборки,
- доверительный интервал для конечной выборки,
По виду критической области:
- двусторонний диапазон: =2*(1-NORMSTRASP(X)nabl))
- =NOORMSTRASP(Xnabl)
- диапазон правой части: =1-NORMSTRASP(Xnabl)
Примеры применения
Расчет средней ошибки выборки при случайном отборе
Расхождение между значениями показателей, полученных по выборке, и соответствующими параметрами генеральной совокупности называется ошибкой репрезентативности. Обозначения основных параметров генеральной и выборочной совокупности.
| Свойства | Основное население | Выборочная совокупность |
| Объем населения (количество единиц) | N | n |
| Количество единиц, обладающих исследуемым качеством (характеристикой) | M | m |
| Процент единиц с исследованным качеством (характеристикой), доля выборки |
| Формулы для средней ошибки выборки | |||
| пассивный отбор проб | без повторной выборки | ||
| для среднего значения | для фракции | для среднего значения | для фракции |
Соотношение между пределом ошибки выборки (Δ), гарантируется с некоторой вероятностью P(t), а средняя ошибка выборки имеет вид: или D = t-m, где t — коэффициент доверия, определяемый в соответствии с уровнем вероятности P(t) матрицей интегральной функции Лапласа.
Формулы расчета численности выборки при собственно-случайном способе отбора
| Процедура отбора | Формулы для определения объема выборки | ||
| для среднего значения | для фракции | ||
| Повторный | |||
| Повторный | |||
Найти численность выборки можно, использовав калькулятор.
2) Для доверительной вероятности: — это значение функции Лапласа соответствует аргументу:. Давайте рассчитаем точность оценки: Определим доверительный интервал: — Этот интервал включает истинное значение с вероятностью 99%.
Типы доверительных интервалов
Существует множество типов доверительных интервалов. Вот самые распространенные из них:
Доверительный интервал для среднего значения — это диапазон значений, который может содержать среднее значение популяции с определенным уровнем доверия. Формула для расчета этого интервала следующая:
Доверительный интервал = x +/- z*(s/ √n )
Доверительный интервал для разницы между средними значениями
Доверительный интервал (ДИ) для разницы между средними — это диапазон значений, который, вероятно, содержит истинную разницу между двумя популяционными средними при заданном уровне доверия. Формула для расчета этого интервала следующая:
Доверительный интервал = ( x 1 — x 2 ) +/- t * √ ((s p 2 /n 1 ) + (s p 2 /n 2 ))
- x 1, x 2 : среднее значение для образца 1, среднее значение для образца 2
- t : t-критическое значение, основанное на уровне доверия и (n 1 + n 2-2) степенях свободы.
- s p 2 : объединенная дисперсия
- n 1, n 2 : объем выборки 1, объем выборки 2
- Объединенная дисперсия рассчитывается следующим образом: s p 2 = ((n 1-1)s 1 2 + (n 2-1)s 2 2 ) / (n 1 + n 2-2)
- Критическое значение t можно определить с помощью калькулятора обратного распределения t.
Доверительный интервал для разницы в пропорциях
Доверительный интервал для разницы в пропорциях — это диапазон значений, который может содержать фактическую разницу между двумя пропорциями населения с заданным уровнем доверия. Формула для расчета этого интервала следующая:
Доверительный интервал = (p 1-p 2 ) +/- z*√(p 1 (1-p 1 )/n 1 + p 2 (1-p 2 )/n 2 ).
Вместо этого мы можем взять простую случайную выборку из 50 черепах и использовать средний вес черепах в этой выборке для оценки истинного среднего значения популяции:
Доверительный интервал для пропорции
Выборочное распределение пропорций имеет биномиальное распределение. Однако, если объем выборки n достаточно велик, то выборочное распределение доли будет приблизительно нормальным со средним значением
Мы оцениваем p=r/n (где r — число индивидов в выборке с интересующей характеристикой) и оцениваем стандартную ошибку:
Мы оцениваем 95% доверительный интервал для этой доли:
Если объем выборки мал (обычно, когда np или n(1-p) меньше 5), то для расчета точных доверительных интервалов необходимо использовать биномиальное распределение.
Если p выражается в процентах, то (1-p) заменяется на (100-p).
Интерпретация доверительных интервалов
При интерпретации доверительного интервала нас интересуют следующие вопросы:
Насколько широк доверительный интервал?
Широкий доверительный интервал указывает на неточность оценки; узкий интервал указывает на точную оценку.
Ширина доверительного интервала зависит от размера стандартной ошибки, которая, в свою очередь, зависит от объема выборки и дает более широкие доверительные интервалы при рассмотрении числовой переменной из изменчивости данных, чем при изучении большого набора данных с небольшим количеством переменных.
Содержит ли CTI значения, представляющие особый интерес?
Можно проверить, находится ли вероятное значение параметра популяции в пределах доверительного интервала. Если да, то результаты соответствуют этому возможному значению. Если нет, то маловероятно (при доверительном интервале 95% вероятность почти 5%), что параметр имеет такое значение.
Если базовые данные популяции не являются нормально распределенными и/или общая дисперсия (дисперсия в популяции) неизвестна, то выборочное среднее следует t-распределению Стьюдента.
Этап 2. Обработка исходной выборки
Обработка выборки статистическими методами требует расчета следующих величин:
1. статистические средние с помощью статистических методов требуют следующих значений: 1.
2. медиана — это число, которое описывает выборку: Ровно половина выборки больше медианы, другая половина меньше медианы.
(для выборки с нечетным числом значений).
3. диапазон — это разница между самым высоким и самым низким значением в выборке.
4. дисперсия — используется для более точной оценки вариации в данных.
5. стандартное отклонение выборки (далее СКО) — наиболее распространенная мера разброса значений подгонки вокруг среднего арифметического.
6. коэффициент вариации — выражает степень разброса значений подгонки.
7. коэффициент осцилляции — отражает относительное колебание крайних значений выборки вокруг среднего.
Таблица 2. Статистические показатели исходной выборки
Индикатор
Значение
Коэффициент вариации, который указывает на однородность данных, составляет 12,29%, но коэффициент осцилляции очень высок. Поэтому мы можем сделать вывод, что исходная выборка неоднородна, поэтому мы можем перейти к расчету доверительного интервала.
Этап 3. Расчёт доверительного интервала
Метод 1: Расчет с использованием медианы и стандартного отклонения.
Доверительный интервал определяется следующим образом: Минимальное значение — среднеквадратичное значение, вычитаемое из медианы; максимальное значение — среднеквадратичное значение, прибавляемое к медиане.
Формула для доверительного интервала:

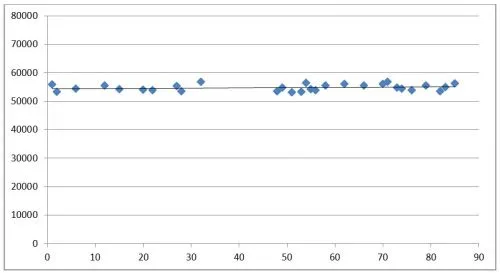
Таким образом, доверительный интервал составляет (47179 до н.э.; 60689 до н.э.).
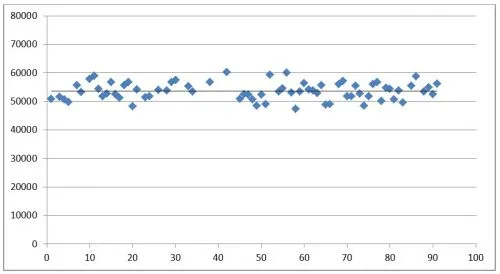
Значения из исходной выборки, которые не попадают в доверительный интервал, удаляются. Двадцать пунктов были удалены, что составляет 22% выборки.
Рисунок 2. Значения, которые попадают в доверительный интервал 1.
Метод 2. Построение доверительного интервала с использованием критического значения t-статистики (коэффициента Стьюдента).
S. В. Грибовский в своей книге «Математические методы оценки стоимости имущества» описывает, как можно рассчитать доверительный интервал с помощью коэффициента Стьюдента. При использовании этого метода оценщик сам должен определить уровень значимости ∝, который определяет вероятность, с которой строится доверительный интервал. Обычно используются уровни значимости 0,1, 0,05 и 0,01. Это соответствует уровням доверия 0,9, 0,95 и 0,99. Этот метод предполагает, что фактические значения математического ожидания и дисперсии практически неизвестны (что почти всегда имеет место в практических задачах оценивания).
Формула для доверительного интервала:

n — размер выборки,
— критическое значение t-статистики (распределение Стьюдента) с уровнем значимости ∝, числом степеней свободы n-1, определяемое по специальным статистическим таблицам или с помощью MS Excel ( →»Статистика»→STUDENT),
∝ — уровень значимости, результат ∝=0,01.
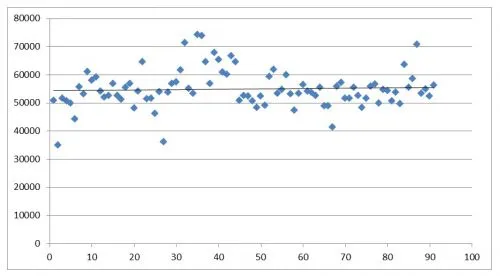
Значения, включенные в исходную выборку, которые не попадают в доверительный интервал, удаляются. Было удалено 62 пункта, т.е. 68% выборки.
Рисунок 2. Значения, попадающие в доверительный интервал 2.