\.(\left|-4< >ight|\ текст)< >=Контактный текст< >ight|\ текст)< >= Полный текст< >ight|\ текст)< >ight|\text< >ight|\ текст)< >\left|-7
Урок 29 Бесплатно Модуль числа
ight||Text

= Полный текст.
Модуль числа (абсолютная величина)
7. \)Практикуйтесь сейчас:.
Чтобы узнать тему нашего урока, попробуйте отгадать загадку.
На этом уроке вы поймете, что называется коэффициентом числа, узнаете его среднее геометрическое, рассмотрите основные свойства коэффициентов, научитесь находить коэффициент числа и применять эти знания к Решение проблем.
Модулус — от латинского «modulus», что означает размер, величина.
Считается, что этот термин впервые ввел английский философ и математик Роджер Коутс, друг и ученик Исаака Ньютона.
Многие ученые использовали понятие фактора в своей научной работе, но только к концу 19 века оно приобрело символическое название.
В 1841 году выдающийся немецкий ученый Карл Теодор Вильгельм Вейерштрасс ввел символическую нотацию для числовых коэффициентов, которая используется и по сей день.
Иногда вместо «коэффициент числа» говорят «абсолютная величина», но важно понимать, что это одни и те же понятия.
Больше информации об этой части курса!
Модуль — это полисемичный термин.
Модуль используется во многих областях человеческой деятельности.
Например, в архитектуре и строительстве единица — это первая мера длины, размер одного из элементов (части здания), т.е. заданное количество.
Квартира — это единица дома, а бетонный блок — единица здания.
Блок позволяет обеспечить пропорциональность структуры, конструкции и их отдельных частей, единообразие формы, координацию частей здания и размеров всего комплекса, а также облегчает установление норм и правил строительства.
В космической технике блоки — это автономные управляющие части космических аппаратов (например, причальные блоки, орбитальные блоки и т.д.).
В радиоэлектронике блок — это автоматизированный и функционально интегрированный узел радиоаппаратуры.
В точных науках и технике единица — это название конкретного коэффициента и величины (например, измерение упругости, измерение сдвига, измерение сопротивления и т.д.).
В версиях модуль — это сетка пространств, которая является основой для компоновки страниц и листов в системах модульной верстки.
Модульные и плавучие конструкции судов становятся все более популярными в судостроительной промышленности.
Секционные блоки или корабельные блоки — это, как правило, повторяющиеся блоки, так называемые модули, которые образуют корпус судна.
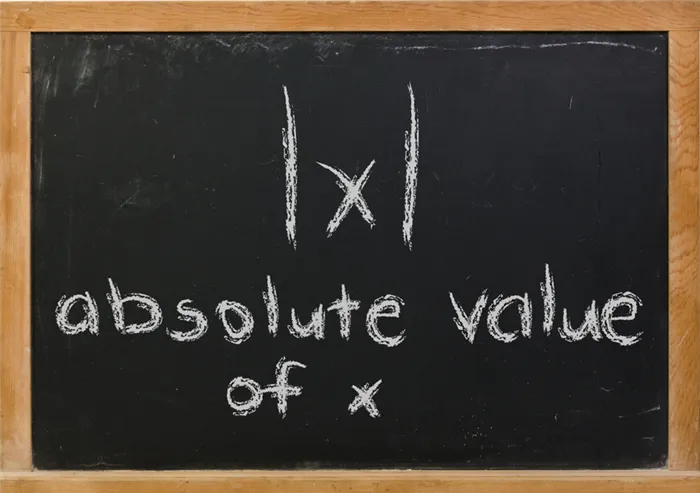
В программировании модуль — это полностью независимая часть программы. Разбиение программы на более мелкие разделы упрощает программу. Секции можно использовать многократно, что упрощает отладку и написание и повышает качество программного кода.
В целом, модуль часто понимается и представляется как начальная единица, компонент, действующий как мера, или как независимая часть системы или структуры.
В математике понятие единства имеет много значений. Давайте узнаем, что в математике называется коэффициентом (абсолютным значением) числа.
Рассмотрим понятие коэффициентов с геометрической точки зрения.
Свойства модуля (абсолютной величины)
Координатная линия описывает вещественное число, и каждому вещественному числу на линии соответствует определенная точка и наоборот. Каждой точке на координатной прямой соответствует вещественное число.
Точки определяются фиксированным расстоянием от начала.
Длина отрезка от начальной точки до точки сохраняет определенное количество единичных отрезков координатной прямой.
Следует рассмотреть некоторые свойства коэффициентов чисел.
1. нулевая мера равна нулю
Нулевая мера равна нулю, потому что нет расстояния от нуля до начала (единичный отрезок 0).
2. модуль числа всегда неотрицательное число (т.е. положительное или нулевое)

По определению, модуль — это расстояние, а модуль положителен, потому что расстояние всегда положительное число.
Мяч вращается на расстояние 3 м вправо по прямой линии, мяч ударяется о стену, останавливается на расстоянии 3 м в противоположном направлении по прямой линии и останавливается.
При каждой остановке шарика координаты точки наносятся на линию координат.
Точка координатной линии — это точка, в которую скатился мяч, начальная точка.
Единицами измерения координатной линии являются 1 деление — 1 метр.
Точка A с координатами A (+ 3) — это момент, когда мяч ударился о стену.
Точка B с координатами b (0) — совпадает с начальной точкой.
Можно ли сказать, что мяч не прошел расстояние, оставаясь сначала спокойным, потому что он перешел на 0 м (от нуля к началу, не соответствуя единичному отрезку)? Определенно нет!
Если бы он вообще не ударил ногой и сохранил спокойствие в этот момент, мяч бы ушел в ноль.
Однако следует понимать, что путь мяча (расстояние) состоит из трех единичных отрезков справа и трех слева.
3 единичные секции + 3 единичные секции = 6 единичных секций
6 отрезков линии = 6 м
Многие ученые использовали понятие фактора в своей научной работе, но только к концу 19 века оно приобрело символическое название.
Поэтому можно сказать, что каждое число состоит из синуса и абсолютного значения (единицы).
Поэтому, чтобы найти коэффициент числа, нужно описать это число без учета синуса.
В этой части урока есть больше информации!
В математике шуточные ассоциации были придуманы для того, чтобы мы могли понять «числовые факторы».
Представьте, что модуль упругости — это ванна, а минус — грязь.
Войдя в ванну (под символом коэффициента), отрицательное число ополаскивается и освобождается от символа. Число выходит из ванны (под символом коэффициента) «чистым» — без символа негатива.
В этом автобусе можно «стирать» положительные, отрицательные и нулевые числа.
Числители противоположных чисел равны.
Рассмотрим это утверждение в качестве примера.
Свойства модуля
Предположим, что коэффициент x равен 4, равно| x | = 4
Отметьте точки на координатной прямой, которые удовлетворяют этому равенству.
Однако все эти оценки имеют смысл только в том случае, если $ 3x -5 \t 0 $. Проверьте это, обменяв цену открытия $ x = \ frac $ при таких условиях.
Модуль, как и все понятия в математике, обладает свойствами.
Свойство 1.| a | > = 0.
Как уже говорилось, модуль игнорирует синус-синус, поэтому он всегда является положительным числом.
Свойство 2. | a | = | -a |.
Это свойство также подтверждает приведенные выше рассуждения. Числители противоположных чисел, т.е. чисел с разными знаками, равны.
Свойство 3. | a | > = a.
Если число A положительное, например, 5, то неравенство | 5 | > = 5 \(⌘ правая стрелка \) 5> = 5, так как знаки неравенства не являются неправильными.
Если число A отрицательное, например, -5, то неравенство| -5 | > = -5 \ (⌘ правая стрелка \) 5> = -5, потому что положительные числа всегда больше отрицательных.<|10|> <|-5|> Свойство 4.| a * b | = | a | * | b |.
Если α = 5 и β = -2, то | 5 * (-2)| = | -10 | = 10, а | 5 | * | -2 | = 5 * 2 = 10, т.е. выражения равны друг другу.
Причина та же, что и для предыдущей собственности. a = 10, b = -5, тогда \(| \ frac | = | -2 |=2 и \frac
= \ frac = 2 \).< 3.
Почему вы увидели неравенства, а не уравнения, как в предыдущих двух свойствах? Давайте рассмотрим два примера.
Пусть a = 1 и b = 2 и | 1 + 2 | = | 3 | =3 и | 1| + | 2 | = 1 + 2 = 3 — неравенство справедливо, так как знаки не точны.Однако если a = -1 и b = 2, то| -1 +2 | = | 1 | =1 и| -1| + | 2 | = 1 + 2 = 3, где 1
Свойство 7.ߡ (ߡ sqrt = | a | | | \).
Докажите это качество. \(⌘ sqrt = x \), тогда x< 0.
потому что квадратный корень не может быть отрицательным. Возведите полученное уравнение в квадрат: a 2 = x 2 a 2-x 2 = 0 (a —x) (a + x) = 0
Из уравнения x = a, a >= 0 из-за ограничения на x.
А из x = -a, по ограничению на x
График модуля
Другими словами, мы получаем уравнение модуля.
Свойство 8.|a| 2 =a2.
Модуль квадрата можно заменить квадратом числа, так как и модуль числа, и квадрат дают положительный результат.
Как представить функцию в терминах ее модуля? Во-первых, давайте разберемся, что делает модуль на графике функции.
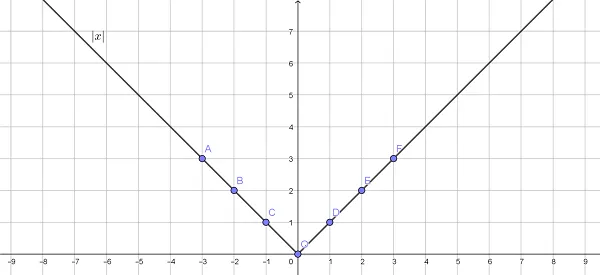
Считайте, что функция y=x- является прямой линией. Y может быть как положительным, так и отрицательным.
Поместите x под символом коэффициента: y = |x|. Теперь y будет положительным. Что происходит с частью графика под осью x? Она зеркально отражена. В итоге мы получаем тик: y = |x|.
Модуль отражает каждый график по отношению к оси x.
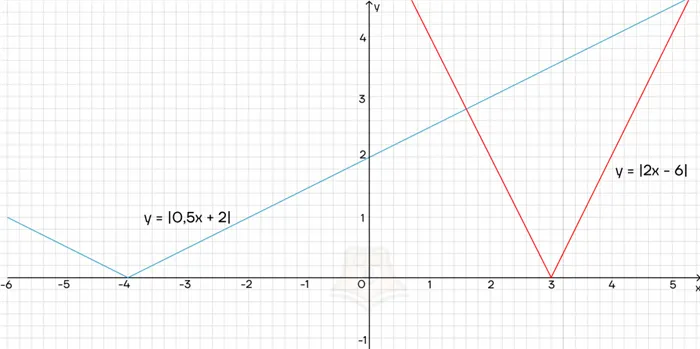
Что произойдет, если перед осью x будет стоять коэффициент? Давайте построим график:.
- если мы прибавляем число, то график сдвигается влево;
- если мы вычитаем число, то график сдвигается вправо.
Клещи станут тоньше и увеличатся. Чем больше коэффициент перед x, тем уже рамка.
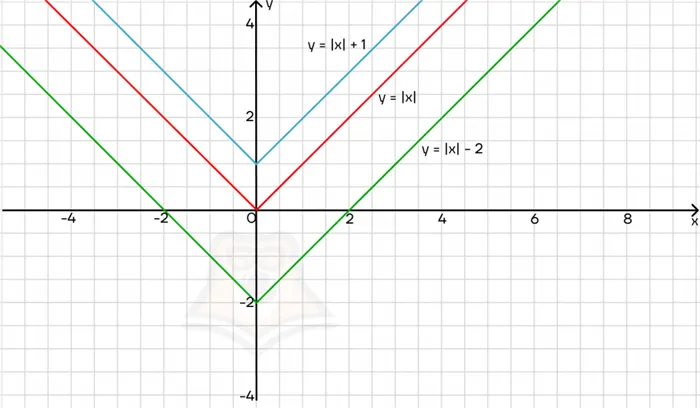
Давайте добавим член в уравнение субъединицы.
График коэффициента перемещается вдоль оси x. Кроме того:.
Уравнения с модулем
Давайте добавим термин к фактору вместо формулы субдиагностики.
График будет перемещаться вдоль оси y.
Все, что вам нужно сделать, это добавить минус перед коэффициентом. Важно, чтобы минус располагался перед устройством, а не внутри него. Затем график зеркально отображается относительно оси x, чуть ниже нее.
1. возьмите уравнение вида|f(x)| =a. Так как мера не может быть отрицательной, то и уравнение не может быть отрицательным. Вы получаете следующие переходы.
Пример 1.Решите уравнение|4x+ 5 | =7.
Решение. Уравнение f(x) = 4x + 5, a = 7. Воспользуемся переходами.
Из первого уравнения x = 0,5, а из второго x = -3.
Ответ: 0,5:-3.
2. в уравнениях и неравенствах можно найти два разных числителя. Что вы делаете в этом случае?
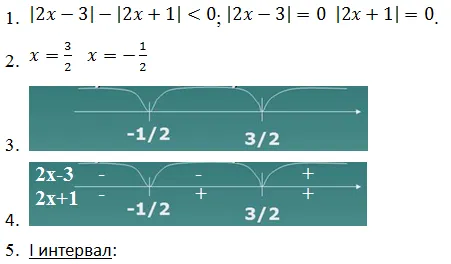
Шаг 1. Найдите нули уравнения слагаемых.
Шаг 2. Постройте числовую линию и найдите точку в промежутке между каждым фактором. Введите отрицательное значение, если уравнение поддиаметра в пространстве отрицательное, или положительное значение, если оно положительное.
Шаг 3: Для каждого интервала разработайте модуль. Если выражение субъединицы в пространстве отрицательное, то раздел расширяется со знаком минус. Если модуль положительный, он дополняется знаком плюс. Важно: Полученные корни должны принадлежать интервалу, на который распространяется мера. В противном случае уравнение не будет решено.
Пример 2: Решите уравнение|x—2 | -| x + 2 | =4x-5.
Решение. Найдите, где числитель равен 0. Поэтому уравнение поддиаметра также должно быть равно нулю.
x-2 = 0 \(⌘ стрелка вправо \)x = 2 x + 2 = 0 \(⌘ стрелка вправо \)x = -2
Проведите прямую линию через эти точки:.
Есть три пробела.
Обратите внимание на первый фактор в интервалах: x > 2 x -2> 0. В результате измеренные значения в первых двух интервалах отрицательны, а в третьем — верны. Поставьте эту отметку красным цветом.
Проанализируйте модуль второго: x + 2> 0 \(⌘ правая стрелка \)x> -2. График положителен во втором и третьем интервалах и отрицателен в первом периоде. Давайте сделаем эту метку синей.
Теперь вы можете увидеть уравнение во всех трех интервалах. Для этого, однако, необходимо ввести ограничение. Полученные точки должны относиться только к этому времени, потому что следующие модули расширяются по-разному.
— (x — 2) — ( — (x + 2)) = 4x -5 -x + 2 + x + 2 = 4x -5 4 = 4x -5 4x = 9 x = 2,25
Точка не удовлетворяет ограничению, потому что она не находится в пространстве (- \ infty \); -2)
Рассмотрим второй интервал: -2; 2). Первая секция удлиняется на минус, вторая — на плюс.
— (x — 2) — (x + 2) = 4x -5 -x + 2 -x -2 = 4x -5 -2x = 4x -5 6x = 5 \ (x = \ frac \)
Эта точка находится в заданном пространстве и является решением уравнения
Рассмотрим третий интервал 2;+\ (⌘ infty \). Обе молекулы растут со знаком плюс, что дает уравнение.
(x — 2) — (x + 2) = 4x -5 x -2 -x -2 = 4x -5 -4 = 4x -5 4x = 1
x = 0,25 — эта точка не находится в пространстве и поэтому не является решением уравнения.
Единственным решением уравнения является \(x = \ frac \).
Как решать уравнения с модулем
При анализе строк в интервале может возникнуть вопрос. Как насчет точек, где мера равна 0? Их обязательно нужно проверить. Это можно сделать индивидуально, либо поменяв местами пункты в уравнении, либо включив их непосредственно в условия выявления факторов.
Уравнения типа |x| = a
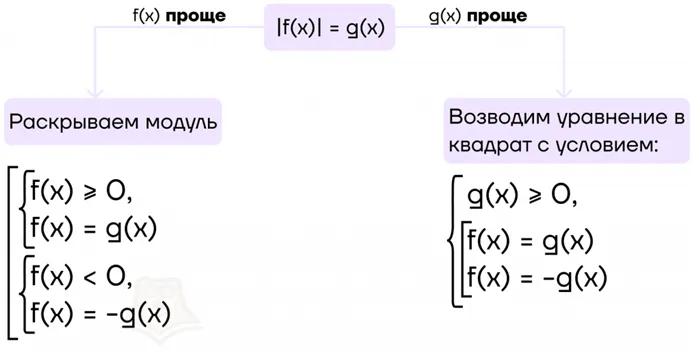
3. составить уравнение| f(x)| = g(x)
Очень просто. Да, это легко. Далее, что такое модуль положительных чисел? Еще проще: модуль положительного числа равен самому числу: $ \ слева | 5 \ справа| = $ 5, $ \ слева | 129,5 \ справа| = $ 129,5 и т.д.
Уравнения с коэффициентами — это равенства, включающие выражения абсолютной величины. В действительных числах он представляет собой расстояние от начала арифметической прямой, но факторное неравенство — это тип неравенства, состоящий из абсолютных величин.
Уравнения типа |x| = |y|
Уравнение | x | = a имеет два ответа x = a и x = -a, оба в прямой координате A с 0.
Если цена отрицательна, то абсолютное уравнение не имеет решения.
| x | для <, где a — числовое расстояние от начала. Это означает, что нам нужно найти все числа, расстояние которых от начала меньше a.
Уравнения типа |x| = y
Если с обеих сторон уравнения присутствуют абсолютные значения, необходимо рассмотреть обе возможности допустимых определений, то есть положительные и отрицательные выражения.
Например, в случае равенства| x -a | = | x + b | есть две возможности: либо (x -a) = — (x + b), либо (x -a) = (x + b).
Решение неравенств с модулем
Затем легко решить эти два уравнения относительно x.
Уравнения вида |x| = a
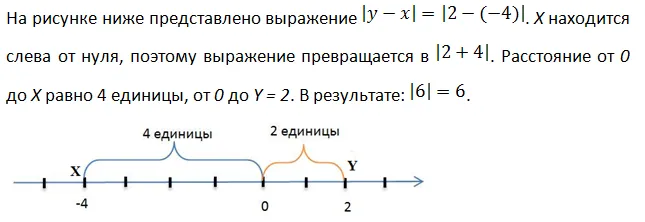
В этом типе уравнения переменная находится слева от нуля, а правая часть содержит окончательное значение выражения неизвестного уравнения. Переменная y может быть больше или меньше нуля.
Чтобы получить ответ на такое уравнение, необходимо решить систему многих уравнений, чтобы убедиться, что y — неотрицательная переменная.
Чтобы лучше понять, как решаются коэффициенты в различных типах уравнений и неравенств, следует разобрать примеры.
Пример 1 (алгебра 6 класса). Решение: | x | + 2 = 4.
Такие уравнения решаются так же, как и уравнения без абсолютных значений. Это означает, что при перемещении неизвестных влево, а фиксированных вправо, уравнение остается неизменным.
Перемещение константы вправо дает. | x | =2.
Поскольку неизвестные связаны с абсолютными величинами, уравнение имеет два ответа, 2 и -2.
Ответы: 2 и -2.
Пример 2 (алгебра 7-й степени). Решаем неравенство |x+ 2 | ≥1.
Первое, что необходимо сделать, это найти точку, в которой изменяется абсолютная величина. Для этого выражение равно 0. Получите x = -2.
Это означает, что -2 — поворотный момент.
Затем определяется знак интервала. В пространстве величина отрицательная, в космосе — положительная.
Пространство разделено на две части.
Общими ответами на эти два неравенства являются интервалы -1 и +∞.
Уравнения вида |x| = |y|
Общим ответом на эти два неравенства является интервал (-∞, -3).
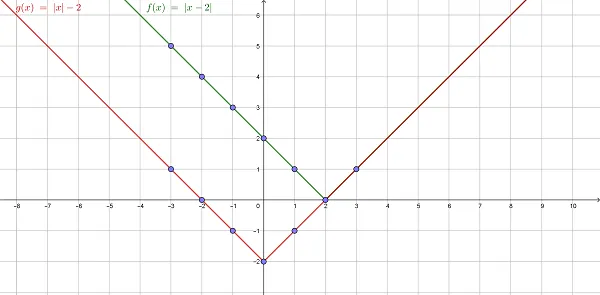
Окончательное решение — объединить ответы из отдельных разделов.
Ответ: x ∈ (-∞, -3 ∪ -1, +∞).

Уравнения вида |x| = y
Пример 1 (алгебра 8-го порядка). Решите уравнение в двух единицах: 2 * | x-1 | + 3 = 9-|x-1|.

Ответ: x1 = 3, x2 = -1.
Пример 2 (Алгебра 8 класса). Решите неравенства:.
Модуль суммы

Пример 1 (алгебра 10-го класса). Находка x:.