Что такое призма — определение и разновидности призм. Что такое призма в жизни?

Содержание

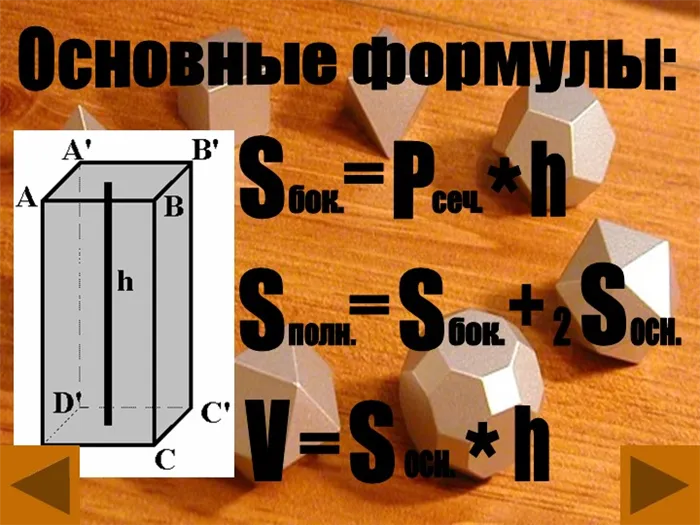
Однако ни одна проблема не может быть решена без формул. Поэтому необходимо рассмотреть некоторые основные формулы, которые можно встретить не только в задачах, но и в жизни.

Призма

Вы когда-нибудь слышали выражение «смотреть сквозь призму чего-то»? Это означает ситуацию, в которой мы воспринимаем что-то под влиянием определенных убеждений или представлений. Сложный, конечно… возможно, потому, что сама призма не является простым понятием. Давайте подойдем к этому математически.

Многие из нас используют стикеры. Записывать, делать закладки, делать заметки. Даже если мы не пользуемся ими, мы наверняка видели их в магазинах или у родственников и друзей.

Такую наклейку можно принять за аэроплан. Теперь давайте вспомним, как выглядит их упаковка. Много-много наклеек накладываются друг на друга, и получается маленькая трехмерная фигурка, верх и низ которой состоят из двух абсолютно одинаковых листов. Вы сразу заметите, что нижняя и верхняя наклейки параллельны друг другу.

Набор наклеек на самом деле не что иное, как призма!

Призма — это многогранник, у которого две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные грани — параллелограммы.

Это определение может показаться немного запутанным, но в нем нет ничего плохого. Чтобы прояснить ситуацию, давайте рассмотрим сложные призмы более подробно.

Строение призмы

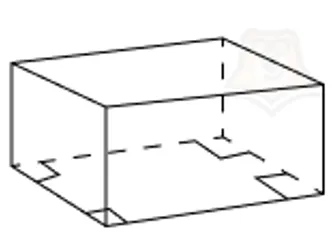
Представьте себе обычную коробку. Его дно и крышка одинаковы и лежат в параллельных плоскостях. Это те же самые многоугольники. Их также называют основанием призмы.

Давайте посмотрим на стенки коробки. Это параллелограммы, только с прямыми углами. Подробнее о параллелограммах вы можете прочитать в статье «Параллелограммы». Эти параллелограммы называются гранями призмы.

Возьмите линейку и измерьте расстояние между основаниями призмы. Из любой точки одного основания проведите перпендикуляр к другому основанию.

Подробнее о расстояниях между плоскостями см. в статьях «Углы в пространстве» и «Расстояния между фигурами».

Возникает вопрос: что мы нашли сейчас? Мы нашли высоту призмы.

Высота призмы — это перпендикуляр, проведенный из любой точки на поверхности основания к другой поверхности основания призмы.

В задачах гораздо удобнее опускать перпендикуляр не из любой точки, а из вершины призмы.

Рассмотрим элементы призмы.

Край — это пересечение двух плоскостей.

Представьте, что вместо картонных стенок у нашей коробки ткань, которую мы должны натянуть в рамке, чтобы коробка не изменилась. В этом случае все прямые линии коробки являются ребрами.

Ребрышки бывают двух видов:

Их также легко отличить друг от друга: Стороны основания являются сторонами многоугольника, который оно содержит, а боковые стороны не являются частью основания.

Боковые грани обладают очень важным свойством: они равны и параллельны друг другу.

Диагональ призмы — это отрезок, соединяющий две вершины призмы, не принадлежащие одной поверхности.

Например, мы можем взять клетку с попугаем и поставить карниз от угла до угла, чтобы птица могла

Виды призм

В первом случае мы рассмотрим призмы по формам в основании. Многоугольник может иметь много сторон, поэтому основанием призмы может быть треугольник, четырехугольник, шестиугольник, десятиугольник и так далее.

Фигуры в основании призмы могут называться по-разному в зависимости от того, как они сформированы. Вот три наиболее важных из них, которые чаще всего встречаются при решении проблем:

Аналогично, каждой призме можно дать название, например, десятиугольная призма или элементарная призма.

Определение призмы гласит, что ее стороны являются параллелограммами. До этого момента мы рисовали только прямоугольники, но на боковых гранях не может быть только прямоугольников.

С этим связана вторая классификация призм. Существует только два типа призм:

Давайте разберемся в них немного подробнее.

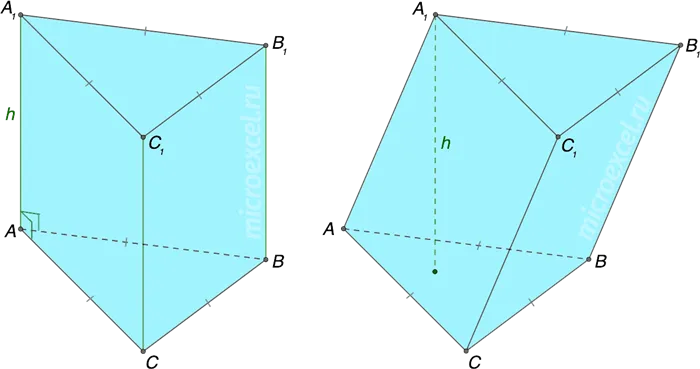
Прямая призма — это призма, боковые грани которой перпендикулярны основанию.

В этом случае боковые края и края основания образуют прямоугольник.

Косая призма — это призма, боковые грани которой образуют угол с основаниями.

Как составить бизнес-план. Для чего нужен бизнес план.

Где можно найти прямую и косую призмы? Как выяснилось, в архитектуре. Типичный жилой дом представляет собой прямую призму. Примером косой призмы является комплекс зданий Gateway Europe в Мадриде.

Давайте рассмотрим прямолинейные призмы немного подробнее. Они довольно распространены и имеют несколько важных характеристик.

Осмотрите свою комнату. Если план квартиры многоугольный, то создается впечатление, что вы сидите на призме. Теперь ответим на вопрос: Как найти высоту помещения?

Простой ответ: измерьте по стене. И если вы посмотрите на угол, то обнаружите, что грань призмы совпадает с высотой. Это дает нам первое свойство линейных призм.

Свойство 1. Высота прямой призмы совпадает с ее боковым ребром.

Рассмотрите стены комнаты, их форму. Они все прямоугольные, верно?

Заморозить 2. Все боковые грани прямоугольной призмы прямоугольные.

Если в основание прямоугольной призмы положить правильный многоугольник, то получится правильная призма.

Прямоугольная призма — это прямоугольная призма, в основании которой лежит прямоугольный многоугольник.

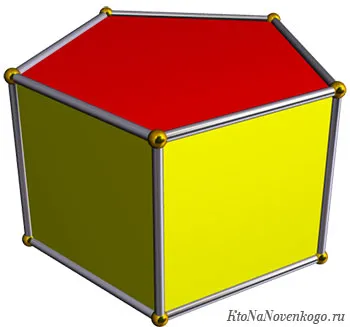
Например, правильная треугольная призма содержит равносторонний треугольник, а правильная шестиугольная призма содержит правильный шестиугольник.

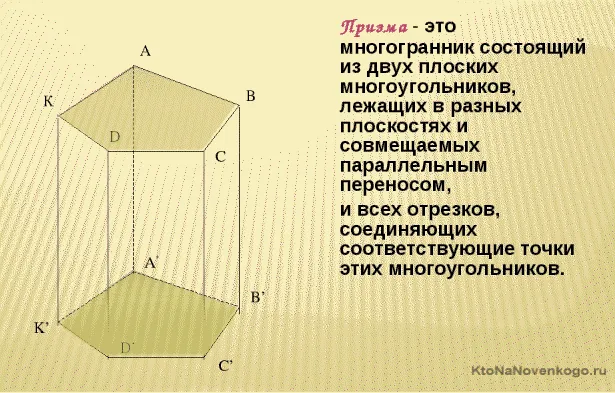
Призма — это геометрическая фигура, представляющая собой трехмерный многогранник. Две его стороны лежат на параллельных основаниях и представляют собой разные многоугольники. А боковые грани — это параллелограммы, соединенные с основаниями.

Классическая призма выглядит так, как показано на рисунке выше.

Призма – это .

На этом рисунке четко показаны все элементы призмы:

В зависимости от типа основания призмы бывают:

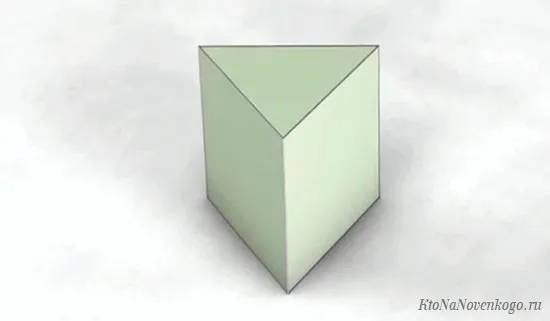
Треугольные — основания содержат два треугольника

Основание – два многоугольника, которые параллельны друг другу;
Боковые грани – четырехугольники, которые скрепляют оба основания и имеют с ними одинаковые грани.

В рамках этой науки Аристотель изучал призмы, кубы, параллелепипеды и другие трехмерные геометрические фигуры.

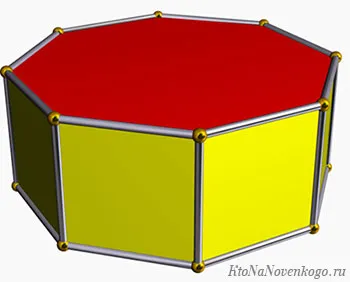
Призма — это твердая (т.е. пространственная) форма, заключенная между несколькими плоскостями. Два из них параллельны друг другу, равны и противоположны. А остальные в любом количестве — параллелограммы.

История изучения призмы

Кстати, само слово «призма» также имеет древнегреческие корни. И означает «призма» — распил. Если смотреть со стороны, призма действительно выглядит как форма, отделенная и вырезанная из чего-то большего. Как будто ствол дерева был распилен на множество стволов.

Например, рассмотрим такую призму.

Она пятиугольная и состоит из следующих элементов:

Любая призма, независимо от типа призмы.

Иногда проявление эго достигает крайней степени: это может быть безусловная любовь к себе в сочетании с абсолютным желанием удовлетворить только свои интересы; возможны также вспышки ненависти к себе или явная апатия к жизни, вплоть до самоубийства. То есть во всех случаях крайнего проявления эго, человек сосредоточен на своих делах и не видит других факторов, если говорить об отношениях, то он не прислушивается к своему партнеру, и рано или поздно отношения разрушаются.

Когда нет ограничивающих факторов, эго может принять невообразимые размеры, и в этом случае эго не только доминирует, но и приобретает полную власть над человеческим разумом и создает соответствующее эгоцентрическое мышление. Более того, эгоцентрический ум развивает определенное восприятие, позволяющее воспринимать все происходящее как единственно возможный вариант.

Элементы призмы

Если человек воспринимает окружающий мир через призму эго и не заинтересован в построении отношений с близкими ему людьми, то шанс встретить «родственную душу» или иметь верных и надежных друзей сводится к минимуму. Такого человека интересуют только его собственные дела и потребности. Эрих Фромм, психоаналитик и известный философ, писал: «Такой человек интересуется только собой, желает только для себя, испытывает удовлетворение не от того, что дает, а от того, что берет». Такого человека не интересует эмоциональное состояние других людей, если только он не может извлечь из этого выгоду, даже если это члены семьи, и он уважает их мнение. А Козьма Прутков говорил, что «эгоист подобен долго сидящему в колодце». Этот человек отвергает важность опыта других людей и считает, что его собственные проблемы являются

Общество осуждает любые проявления эгоизма, и способность жертвовать своими интересами ради интересов других людей вызывает искреннее восхищение. Но действительно ли все так просто?

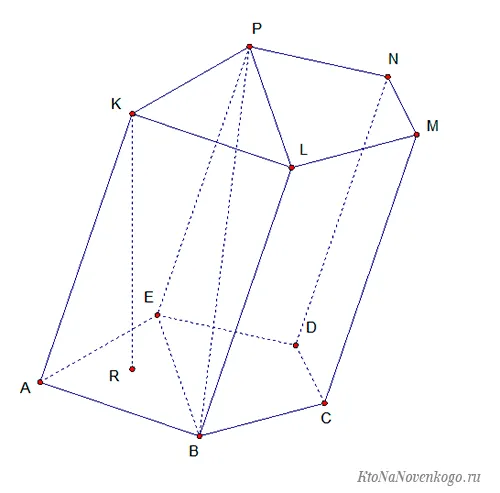
Основание – их, как и положено, две штуки, в данном случае это пятиугольники ABCDE и KLMNP;
Боковая грань – их количество равно количеству углов оснований, то есть тоже пять. Это параллелограммы ABKL, BCLM, CDMN, DENP и EAPK;
Боковая поверхность – так называют сумму всех имеющихся боковых граней, которые мы перечислили выше;
Полная поверхность – это сумма всех частей призмы;
Боковое ребро – линии соединения боковых граней. В нашем случае это отрезки KA, LB, MC, ND и PE;
Высота – отрезок, который соединяет основания призмы под прямым углом. В нашем случае KR. Это касается наклонных призм, у которых грани не перпендикулярны основаниям. В противном случае, высота совпадает с боковым ребром;
Диагональ – отрезок (PВ), который соединяет две вершины призмы, не относящиеся к одной грани;
Диагональная плоскость – плоскость, которая проходит через основание, боковую грань и диагональ. В нашем случае это BPE и BPL;
Диагональное сечение – плоскость, которая образуется пересечением призмы и диагональной плоскостью. В нашем случае это параллелограмм BLPE. В частных случаях она может быть ромбом или квадратом.

Какой бизнес у Андрея Ковалева: на чем зарабатывает лидер группы «Пилигрим». Андрей ковалев миллиардер на чем заработал.

Питер Шварц, почетный научный сотрудник и член правления Института Айн Рэнд, в своей недавней книге «В защиту эгоизма: почему не стоит жертвовать собой ради других» излагает мифы об эгоизме и говорит, что каждый человек имеет неоспоримое право использовать результаты своей деятельности для собственной выгоды.

Проблема восприятия действительности через призму Эго

Наше восприятие окружающего мира формируется под влиянием концепций. В сознании большинства людей не существует такого понятия, как «хороший эгоизм».

Категоричность такой концепции термина «эго» в некотором смысле искажает его истинный смысл («действовать в собственных интересах, руководствуясь голосом разума»).

Отношение к этому аспекту также связано с историей. В древние времена люди не обвиняли друг друга в эгоцентризме: Цивилизация была еще очень молодой, поэтому внимание человека к себе и его самосознание соответствовали его знаниям об окружающем мире. С приходом христианства эгоизм стал отрицательным качеством человеческого характера. Христианский идеал человека, Иисус Христос, был альтруистом. Но в эпоху Возрождения и Просвещения, когда каждый человек приобрел особую ценность, внимание к идеям и потребностям личности вновь перестало быть негативной чертой. А в 19 веке, когда в Европе набирал силу капитализм, было высказано мнение, что невозможно выжить в конкурентном обществе, не учитывая собственные интересы.

Более того, даже сегодня в Р. Ф. корысть превратилась из осуждаемого понятия в признанное. И эта двухсторонняя концепция эгоизма несколько сбивает с толку. «Несовместимость двух принципов («эгоизм — плохо» и «эгоизм — хорошо»), проповедуемых в одной и той же культуре, приводит к глубокому личностному конфликту, — говорит философ Ирина Рудзит.

Эрих Фромм считал, что «полное отсутствие эгоизма является одним из его признаков, и часто самым важным. Философы давно ставят под сомнение существование рационального эгоизма. Такой эгоист не жертвует своими интересами, но и не пытается манипулировать всем вокруг, чтобы весь мир вращался вокруг него. Он удовлетворяет свои собственные рациональные желания и готов делиться всем, что выходит за рамки обычных потребностей. «Это человек с достаточно высокой самооценкой, который знает, что он имеет право на определенные льготы, — объясняет Светлана Кривцова, — его самооценка и

Например, многие рефлексы, такие как «территориальная агрессия» или защита территории, являются оправданным поведением, когда мы наблюдаем за реакцией представителей животного мира, но когда речь идет о человеке, мы должны ожидать свободы действий и выбора в его реакции на мнение других.

Как найти грань между здоровыми проявлениями эго и чрезмерной концентрацией эгоистических устремлений?

Когда мы не можем свободно реагировать на мнение других, происходит вот что: Если кто-то говорит что-то неприятное о нашей внешности, творчестве и т.д., у нас сразу пропадает желание и падает самооценка. Такая реакция на мнение окружающих значительно усложняет нашу жизнь и препятствует дальнейшему развитию.

Давайте рассмотрим варианты схемы треугольника.

Дополнительная скидка: 15% (только до 31 декабря)

К этой скидке мы можем добавить скидку для вашего учебного заведения (в зависимости от того, сколько ваших коллег прошли курс «Инфоурок»).

В настоящее время 54 936 учреждений предлагают накопительную скидку (от 2% до 25%). Чтобы узнать, какая скидка распространяется на всех сотрудников вашего учреждения, войдите в личный кабинет Инфорурок.

PBN, RNP, B-RNAV, P-RNAV. Pbn что это такое?

Курс переподготовки

Дополнительная скидка: 15% (только до 31 декабря)

К этой скидке мы можем добавить скидку для вашего учебного заведения (в зависимости от того, сколько ваших коллег участвовали в курсах «Инфорурок»).

1 слайд В мире призм! Дизайн.

Эссе должно содержать информацию о призме, как о теории, так и много другой интересной информации об использовании этой формы во всех сферах жизни общества. — Аннотация — Программа Программа должна представлять основные формулы и применять их в основном для решения основных проблем, быть простой и доступной — Презентация Презентация дает краткий обзор всего проекта и описывает основные цели, задачи и конечный результат.

Что будет происходить, если вас лишить свободы реакции?

3 слайд Цель задания: выполнить задачи задания. (Эссе, программа, презентация) Совершенствовать навыки использования различных компьютерных программ. Они узнают много новой и полезной информации о призме не только для школы, но и для своего общего развития.

4 Прозрачность Чтобы добиться успеха, студенты должны догнать своих предшественников, а не ждать отстающих. (Аристотель) Некоторые типы призм: a) правильная прямая шестиугольная призма. b) правильная косая шестиугольная призма. c)Прямая косая квадратная призма. d)Прямая квадратная призма (параллелограмм).

Виды призм

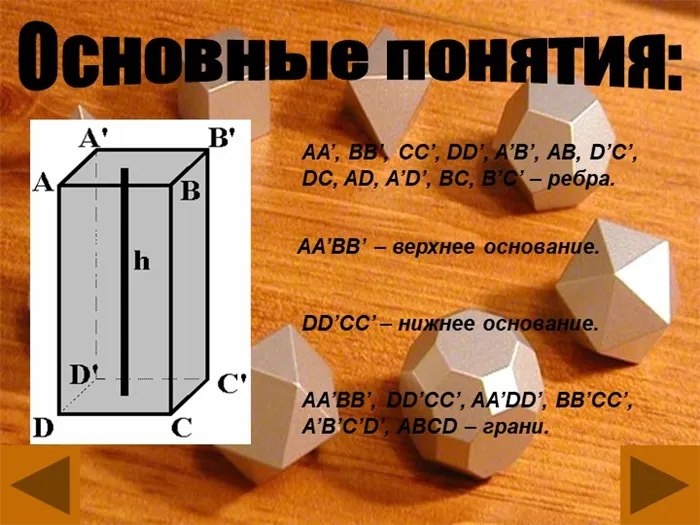
5 слайдов Основные термины: AA’, BB’, CC’, DD’, A’B’, AB, D’C’, DC, AD, A’D’, BC, B’C’ — края.

Прямая призма – боковые грани расположены под прямым углом к основаниям (т.е. перпендикулярны им). Высота такой фигуры равняется ее боковому ребру.
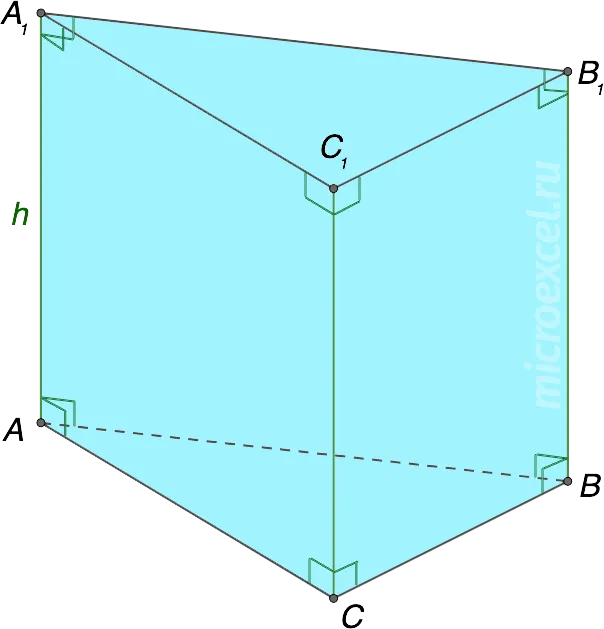
Наклонная призма – боковые грани фигуры не перпендикулярны ее основаниям.
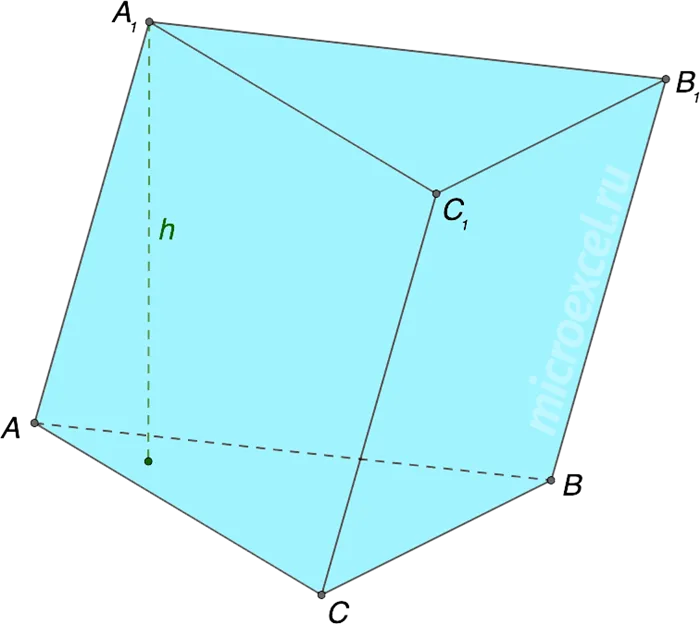
Правильная призма – основаниями являются правильные многоугольники. Может быть прямой или наклонной.
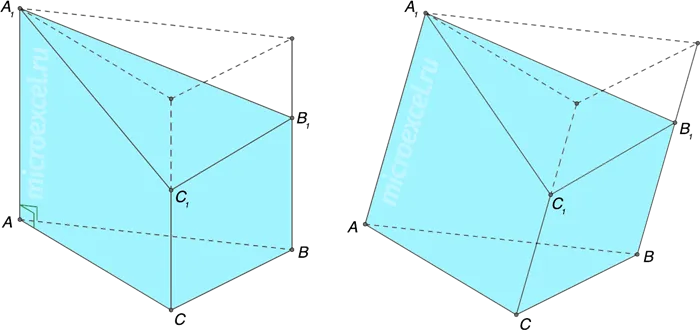
Усеченная призма – часть фигуры, оставшаяся после пересечения ее плоскостью, не параллельной основаниям. Также может быть как прямой, так и наклонной.