Кластеризация это что такое. Кластеризация это что такое?

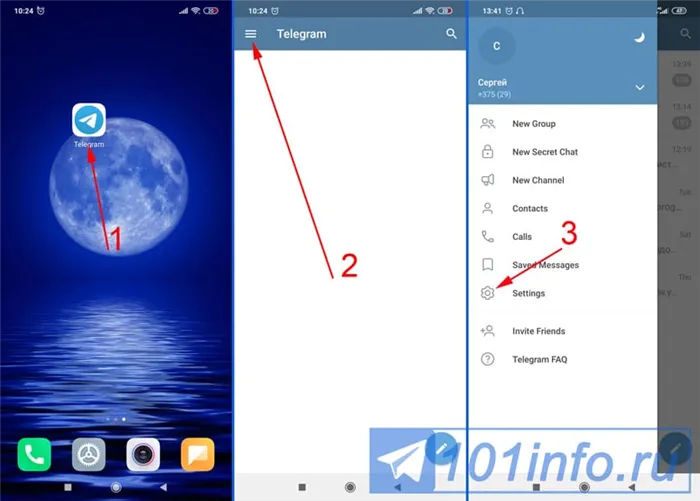
Если удалить связь с меткой CD длиной 6 единиц (ребро с наибольшим расстоянием), то получатся два кластера: и. Второй кластер можно разделить еще на два кластера, удалив ребро EF, длина которого составляет 4,5 единицы.

Обзор алгоритмов кластеризации данных

В своей диссертации я изучал и сравнивал алгоритмы кластеризации данных. Я подумал, что уже собранный и обработанный материал может быть кому-то интересен и полезен. Что такое кластеризация, описано sashaeve в статье «Кластеризация: алгоритмы k-means и c-means». Я частично повторю слова Александра и частично дополню их. Те, кого заинтересовала статья, могут также ознакомиться со ссылками в списке литературы в конце статьи.

Я также попытался перенести сухой стиль «Диплома» на более журналистский стиль.

Понятие кластеризации

Кластеризация (или кластерный анализ) — это задача разделения набора объектов на группы, называемые кластерами. В каждой группе должны быть «похожие» объекты, а объекты в разных группах должны быть как можно более разными. Основное отличие кластеризации от классификации заключается в том, что список кластеров не является точно заданным и определяется в процессе работы алгоритма.

1. Отбор выборки объектов для кластеризации.
2. Определение множества переменных, по которым будут оцениваться объекты в выборке. При необходимости – нормализация значений переменных.
3. Вычисление значений меры сходства между объектами.
4. Применение метода кластерного анализа для создания групп сходных объектов (кластеров).
5. Представление результатов анализа.

Меры расстояний

Как же определяется «сходство» объектов? Сначала нам нужно создать вектор признаков для каждого объекта — обычно это набор числовых значений, например, рост и вес человека. Однако существуют также алгоритмы, которые работают с качественными (категориальными) атрибутами.

После определения вектора признаков мы можем выполнить нормализацию, чтобы все элементы вносили одинаковый вклад в расчет «расстояния». Нормализация предполагает приведение всех значений к определенному диапазону, например, -1, -1 или 0, 1.

Наконец, для каждой пары объектов измеряется «расстояние» между ними — степень похожести. Существует множество метрик, вот лишь основные из них:

1. Евклидово расстояние Наиболее распространенная функция расстояния. Представляет собой геометрическим расстоянием в многомерном пространстве:
2. Квадрат евклидова расстояния Применяется для придания большего веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом:
3. Расстояние городских кварталов (манхэттенское расстояние) Это расстояние является средним разностей по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Однако для этой меры влияние отдельных больших разностей (выбросов) уменьшается (т.к. они не возводятся в квадрат). Формула для расчета манхэттенского расстояния:
4. Расстояние Чебышева Это расстояние может оказаться полезным, когда нужно определить два объекта как «различные», если они различаются по какой-либо одной координате. Расстояние Чебышева вычисляется по формуле:
5. Степенное расстояние Применяется в случае, когда необходимо увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Степенное расстояние вычисляется по следующей формуле: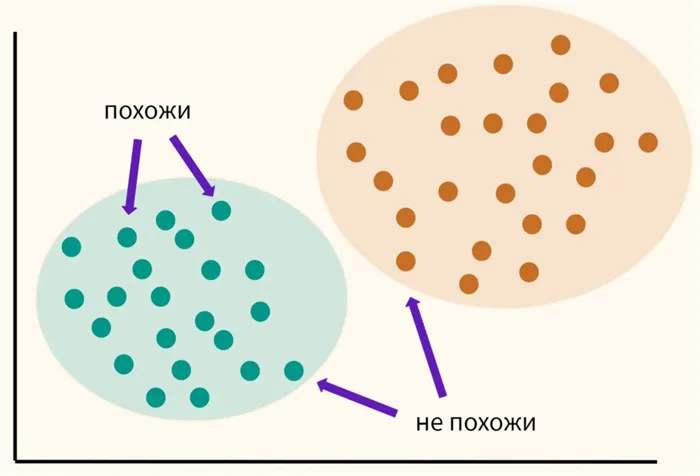, где r и p – параметры, определяемые пользователем. Параметр p ответственен за постепенное взвешивание разностей по отдельным координатам, параметр r ответственен за прогрессивное взвешивание больших расстояний между объектами. Если оба параметра – r и p — равны двум, то это расстояние совпадает с расстоянием Евклида.

Выбор метрики остается полностью на усмотрение исследователя, так как результаты кластеризации могут значительно отличаться при использовании различных мер.

Типы входных данных

Признаковое описание объектов

Объект описывается набором атрибутов. Атрибуты могут быть числовыми и категориальными. Например, можно кластеризовать группу клиентов на основе их покупок в интернет-магазине. Вводятся средний доход, возраст, количество покупок в месяц, предпочитаемая категория покупок и другие критерии.

Матрица расстояний между выделенными объектами

Это симметричная таблица со строками и столбцами, в которых перечислены элементы, пересечение которых указывает на расстояние между ними: например, таблица расстояний между гостиницами в разных городах. Такой метод может помочь определить группы отелей, которые находятся в одном и том же месте.

Цели кластеризации

Сжатие данных

Кластеризация полезна, когда исходная выборка очень велика. Это оставляет по одному типичному представителю от каждого кластера. Количество кластеров может быть произвольным — здесь важно, чтобы количество кластеров не было слишком большим.

Поиск паттернов внутри данных

2. подходы для систем искусственного интеллекта. Большая условная группа методов, различающихся в методологическом отношении.

Поиск аномалий

4. Иерархический подход. Предполагает существование вложенных групп — кластеров разного порядка. Различие между алгоритмами кластеризации и разделения (объединение и разделение). В зависимости от количества атрибутов различают многоатрибутные (когда сравниваются несколько атрибутов одновременно) и одноатрибутные методы классификации (когда применяется один атрибут).

Методы кластеризации

Чтобы показать, как работает алгоритм кластеризации, возьмем другой классический набор данных из библиотеки Sklearn, а именно данные о цветке радужной оболочки глаза.

Давайте сразу загрузим данные и преобразуем их в формат набора данных из библиотеки Pandas.

• EM-алгоритм применяется для нахождения оценок максимального правдоподобия параметров вероятностных моделей (если есть зависимость от скрытых переменных).
• K-средних — алгоритм минимизирует суммарное квадратичное отклонение точек кластеров от их центров.
• Алгоритмы семейства FOREL основаны на идее объединения объектов в один кластер в областях их максимальной концентрации.

# Импортируйте набор данных из раздела dataset библиотеки Sklearn.

• Метод нечеткой кластеризации C-средних предполагает разбиение имеющегося множества элементов на определенное число нечетких множеств. Метод является усовершенствованным вариантом К-средних.
• Нейронная сеть Кохонена — класс нейронных сетей со слоем Кохонена, состоящим из линейных формальных нейронов.
• Генетический алгоритм — алгоритм поиска, применяемый для решения задач оптимизации и моделирования с помощью случайного подбора, вариации и комбинирования искомых параметров. Используются механизмы, аналогичные естественному отбору в природе.

# Создайте набор данных, получите данные из iris.data и имена столбцов из iris.feature_names.

Практический пример — цветы ириса

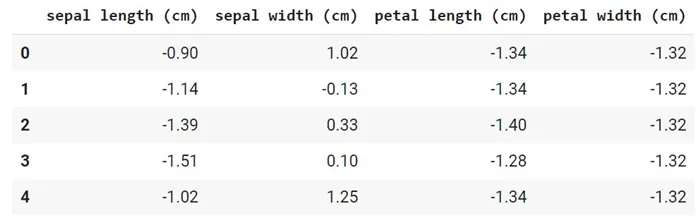
iris_df = pd. DataFrame ( iris. data, columns = iris. feature_names )

Этап 1. Загрузка данных

Это набор данных из 150 образцов цветов ириса, разделенных на три вида (Iris setosa, Iris virginica и Iris versicolor), каждый из которых состоит из 50 растений. Каждый экземпляр описан с помощью четырех характеристик (длина и ширина чашелистика и длина и ширина лепестка).

Мы намеренно не использовали целевую переменную, поскольку решаем задачу кластеризации и предполагаем, что заранее не знаем, на какие группы или кластеры успешно разделятся наши данные.
С другой стороны, тот факт, что мы заранее знаем, что существует три типа, помогает нам оценить качество кластерного анализа (см. ниже).
Давайте сначала проверим, есть ли недостающие значения.

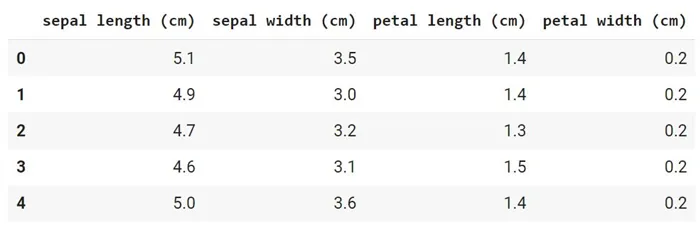
Мы видим, что отсутствующих значений нет. Набор данных был предварительно обработан.

Кроме того, у нас нет категориальных переменных. Это видно из результата работы функции head().

Остается только вопрос о сфере применения атрибутов. Как упоминалось ранее, в методе k-means нормализация данных имеет особое значение. Даже небольшая разница в масштабе атрибутов может повлиять на конечный результат.

Этап 2. Предварительная обработка данных

# Импортируйте необходимый класс из модуля препроцессинга библиотеки Sklearn.

# Восстановить кадр данных с нормализованными значениями

iris_df_scaled = pd. DataFrame ( iris_scaled, columns = iris. feature_names )

Для кластерного анализа мы берем все имеющиеся у нас данные.

# Все характеристики оставлены как есть, а данные для наглядности вставлены в переменную X.
Наиболее важным вопросом, с которым нам приходится сталкиваться на этапе обучения модели, является выбор количества кластеров.
Количество кластеров в методе k-means — это так называемый гиперпараметр, т.е. параметр, который должен быть установлен перед обучением модели.

Этап 3 и 4. EDA и отбор признаков

Усложним нашу задачу и сделаем вид, что у нас нет специальных знаний о количестве типов радужки (мы знаем, что их три). Поэтому мы должны использовать метод локтя.

# Создайте пустой список для захвата индекса WCSS (наша ошибка).

Этап 5.1. Обучение модели

# Используйте новую для нас функцию range(), которая возвращает последовательность чисел.

# настроить параметры модели (подробнее об этом позже)

kmeans = KMeans ( n_clusters = i, init = ‘k-means++’, max_iter = 300, n_init = 10, random_state = 42 )

При решении задач кластеризации мы берем данные, проверяем их масштаб и выбираем количество кластеров (используя экспертную оценку или метод локтя). К сожалению, из-за отсутствия разделов бывает очень трудно дать точную оценку качества кластеризации.
Почему кластеризацию называют машинным обучением без учителя?
Посмотреть правильный ответ

Ответ: В таких задачах нет целевой переменной, нет сегментации. Алгоритм пытается структурировать данные, о которых мало что известно заранее.

Подведем итог

Как выбирается гиперпараметр модели (количество кластеров)?

Вопросы для закрепления

Посмотреть правильный ответ

Ответ: Есть два способа: (1) мнение эксперта и (2) метод локтя.

Каковы основные ограничения модели k-means?

Смотрите правильный ответ

Ответ: Есть два способа: (1) мнение эксперта и (2) метод локтя.

Дополнительные упражнения⧉ можно найти в конце брошюры.

В заключение третьего раздела мы рассмотрим классические алгоритмы машинного обучения. Пора переходить к более сложным задачам. Давайте начнем с рекомендательных систем.

Ответ: Есть два способа: (1) мнение эксперта и (2) метод локтя.

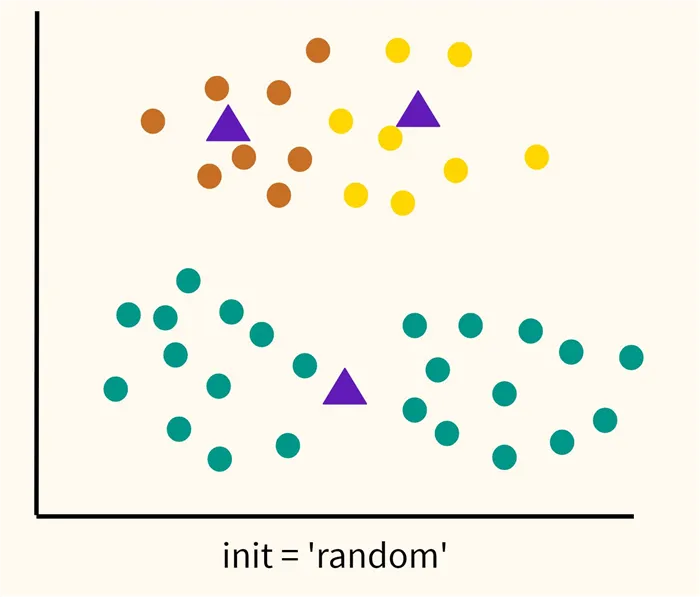
Ответ Давайте посмотрим. Сначала рассмотрим случайную инициализацию центроида ( init = ‘random’ ). Как следует из формулировки, мы случайным образом выбираем центры кластеров, а затем алгоритм пытается минимизировать функцию потерь (в данном случае WCSS), как описано в лекции.

У этого подхода есть один недостаток. Если центры кластеров расположены слишком близко друг к другу, алгоритм может «разделить» то, что должно быть одним кластером, и «объединить» два разных кластера. Пример неправильной кластеризации показан на рисунке ниже.

Как мы видим, алгоритм действительно минимизировал WCSS, но только в той степени, в которой позволял первоначальный выбор расположения центроида. Это так называемый локальный минимум функции потерь. Глобальный минимум не был найден. Схематично глобальный минимум будет выглядеть следующим образом.

Ответы на вопросы

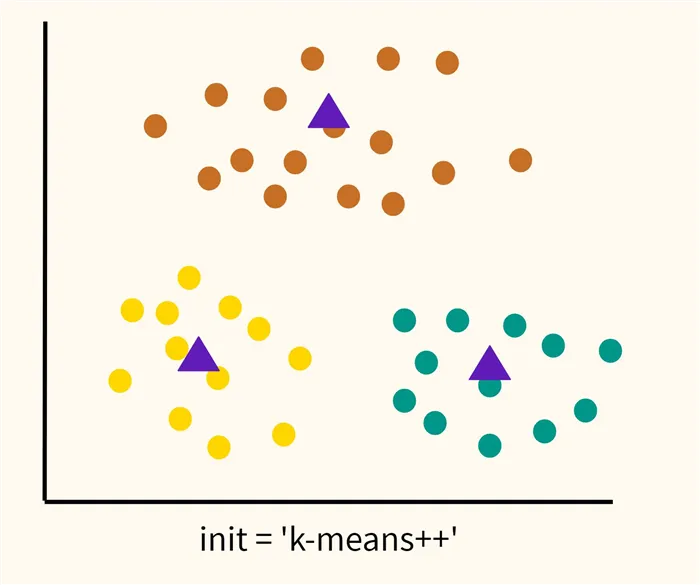
В этом случае глобальный оптимум будет достигнут путем максимизации начального расстояния до центра тяжести, на чем и основан метод k-means++ (‘init = ‘k-means++’).

Сам алгоритм k-means++ очень прост:

В этом алгоритме количество кластеров задавать не нужно: Он определяется автоматически. Вместо этого нужно указать радиус поиска точек и минимальное количество точек в кластере.

Почему мы используем различные подходы для кластеризации? На самом деле, не существует правильного способа разделения объектов на кластеры. Разные методы подходят для разных задач, и применение нескольких методов к одному и тому же набору данных может выявить различные характеристики набора данных. Например, если есть объекты, которые не принадлежат ни к одной группе, а кластеры могут иметь сложную форму, лучше использовать DBSCAN. Метод K-Means предпочтителен, когда количество кластеров составляет

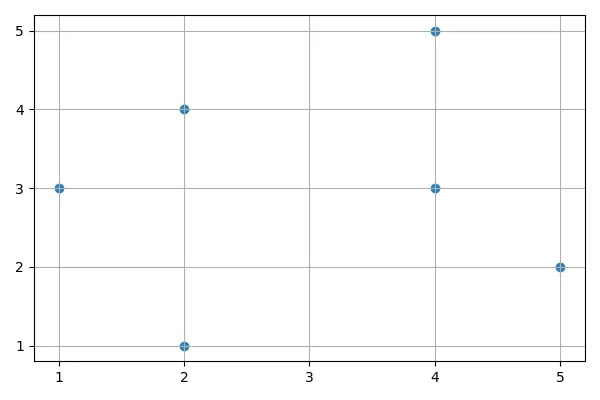
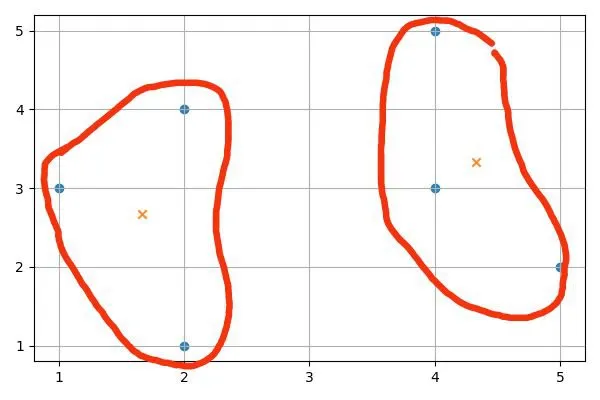
Если вы используете K-Means с двумя кластерами, вы получите следующее распределение:

В конце алгоритма средние точки находятся в точках 4 1/3, 3 1/3, 1 2/3, 2 2/3 (отмечены крестиками на рисунке). Точки 2, 4, 1, 3, 2, 1 находятся в одном кластере, а 5, 2, 4, 3, 4, 5 — в другом.

1. Первый центроид выбирается случайно.
2. Далее рассчитывается Евклидово расстояние между этим центроидом и всеми остальными точками датасета. Наиболее удаленная точка станет следующим центроидом.
3. Каждая точка относится к ближайшему выбранному центроиду.
4. Точка, наиболее удаленная от «своего» центроида, становится следующим центром кластера.
5. Повторяем шаги 3 и 4 до тех пор, пока не выявим k центроидов.

DBSCAN

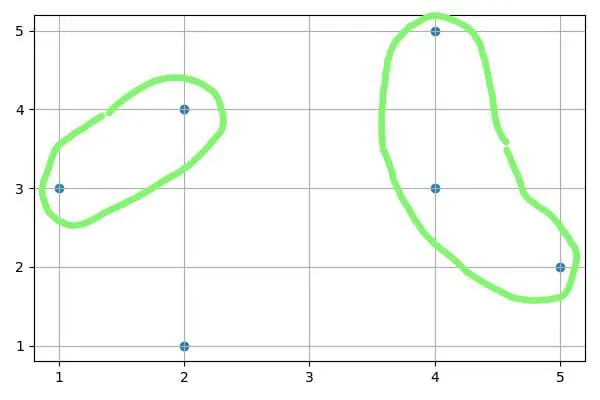
Если вы используете DBSCAN с радиусом 2 и минимальным количеством точек в кластере 2, вы получите два кластера и одно отклонение:

1. Выбираем случайную точку-объект выборки и ищем точки вокруг нее в выбранном нами радиусе.
2. Если на предыдущем этапе набралось меньше точек, чем минимальное нужное нам количество, помечаем все эти точки как выбросы: будем считать, что они не принадлежат ни одному кластеру
3. Если набралось достаточное количество точек, для каждой из них также ищем новые точки в определенном нами радиусе. Таким образом, все точки, находящиеся друг от друга на расстоянии меньшем или равном заданному радиусу будут образовывать один кластер

Для точки 1, 3 радиуса 2 найдена точка 2, 4; для точки 4, 5 сначала найдена точка 4, 3, а затем точка 5, 2. Точка 2, 1 не имеет соседей с расстоянием менее 2.

Кластеризация, группировка похожих объектов, является одной из основных задач анализа данных и добычи данных. Список областей применения велик: сегментация изображений, маркетинг, обнаружение мошенничества, прогнозирование, анализ текста и многие другие. В настоящее время кластеризация часто является первым шагом в анализе данных. После выявления схожих групп применяются другие методы, и для каждой группы создается отдельная модель.

Пример

Кластеризация была сформулирована в той или иной форме в таких научных областях, как статистика, распознавание образов, оптимизация и машинное обучение. Отсюда и множество синонимов для понятия кластеризации — класс, таксономическая единица, плотность.

На сегодняшний день количество методов разбиения групп объектов на кластеры достаточно велико — несколько десятков алгоритмов и еще больше их модификаций. Однако нас интересуют алгоритмы кластеризации с точки зрения их применения в добыче данных.

Кластеризация при добыче данных приобретает ценность, когда она служит одним из этапов анализа данных, построения полного аналитического решения. Аналитику часто проще выбрать группы похожих объектов, изучить их характеристики и построить отдельную модель для каждой группы, чем строить общую модель для всех данных. Эта техника постоянно используется в маркетинге для определения групп клиентов, покупателей и продуктов и разработки отдельной стратегии для каждой из них.

Данные, с которыми сталкивается технология добычи данных, очень часто имеют следующие важные характеристики:

Все атрибуты или свойства объектов дифференцируются на числовые и категориальные. Числовые атрибуты — это те, которые можно классифицировать в пространстве, категориальные атрибуты, соответственно, те, которые не поддаются классификации. Например, атрибут «возраст» является числовым, а «цвет» — категориальным. Присвоение значений атрибутам выполняется во время измерений с выбранным типом шкалы и обычно является отдельной задачей.

Введение

В большинстве алгоритмов кластеризации объекты сравниваются на основе определенной степени близости (homo

Алгоритм, удовлетворяющий этим требованиям (особенно второму), называется масштабируемым. Масштабируемость — это важнейшее свойство алгоритма, которое зависит от вычислительной сложности и программной реализации. Существует и более широкое определение. Алгоритм считается масштабируемым, если время его выполнения линейно увеличивается с ростом числа записей в базе данных при фиксированном объеме оперативной памяти.

Однако не всегда есть необходимость обрабатывать чрезвычайно большие таблицы данных. По этой причине на заре теории кластерного анализа вопросам масштабируемости алгоритма почти не уделялось внимания. Предполагалось, что все обрабатываемые данные поместятся в основной памяти, и основное внимание всегда уделялось улучшению качества кластеризации.

Кластеризация в Data Mining

Трудно достичь баланса между качественной кластеризацией и масштабируемостью. Поэтому арсенал интеллектуального анализа данных в идеале должен включать как эффективные алгоритмы кластеризации для микрочипов, так и масштабируемые алгоритмы для обработки очень больших баз данных.

Таким образом, мы уже можем провести классификацию на масштабируемые и немасштабируемые алгоритмы кластеризации. Продолжим классификацию.

• высокая размерность (тысячи полей) и большой объем (сотни тысяч и миллионы записей) таблиц баз данных и хранилищ данных (сверхбольшие базы данных);
• наборы данных содержат большое количество числовых и категорийных атрибутов.

В зависимости от метода кластеризации алгоритмы можно разделить на два типа: иерархические и неиерархические. Классические иерархические алгоритмы работают с признаками категорий только в том случае, если построено полное дерево вложенных кластеров. Это обычные кумулятивные методы построения кластерных иерархий — они осуществляют последовательное объединение исходных объектов и соответствующее уменьшение числа кластеров. Иерархические алгоритмы обеспечивают относительно высокое качество кластеризации и не требуют предварительного задания количества кластеров. Большинство из них имеют сложность O(n^2) .

Неиерархические алгоритмы основаны на оптимизации объективной функции, определяющей оптимальное разбиение множества объектов на кластеры в рамках определенной концепции. К этой группе относятся популярные алгоритмы семейства k-means (k-means, fuzzy c-means, Gustafson-Kessel), которые используют в качестве объективной функции сумму квадратов взвешенных отклонений координат объектов от центров искомых кластеров.

Кластеры имеют сферическую или эллипсоидную форму. В обычном применении минимизация функции основана на методе множителей Лагранжа и позволяет искать только ближайший локальный минимум. Использование методов глобального поиска (генетические алгоритмы) значительно увеличивает вычислительную сложность алгоритма.

Среди неиерархических алгоритмов, которые не полагаются на расстояние, есть алгоритм EM (Expectation-Maximisation), который вместо центров кластеров использует функцию плотности вероятности для

1. Минимально возможное количество проходов по базе данных;
2. Работа в ограниченном объеме оперативной памяти компьютера;
3. Работу алгоритма можно прервать с сохранением промежуточных результатов, чтобы продолжить вычисления позже;
4. Алгоритм должен работать, когда объекты из базы данных могут извлекаться только в режиме однонаправленного курсора (т.е. в режиме навигации по записям).

Первый атрибут — числовой, остальные — категориальные. Если мы хотим использовать классический иерархический алгоритм с любой мерой сходства, мы должны каким-то образом обесценить атрибут «возраст». Например, вот так:

Таким образом, мы, конечно, потеряем часть информации. Если мы определяем расстояние в евклидовом пространстве, возникают проблемы с атрибутами категорий. Видно, что расстояние между атрибутами «пол мужской» и «пол женский» равно 0, так как значения этого атрибута находятся на шкале имен. А атрибут «образование» может быть измерен либо по шкале имен, либо по шкале классов, при этом каждому значению присваиваются определенные баллы.

Какой вариант мне следует выбрать? Что если атрибуты категории более важны, чем числовые атрибуты? Решение этих проблем зависит от аналитика. Более того, при использовании алгоритма k-means и подобных алгоритмов возникают трудности с пониманием центров кластеров признаков категорий и определением количества кластеров заранее.

Алгоритмы кластеризации: блеск и нищета

Алгоритм оптимизации объективной функции в алгоритмах, основанных на неиерархических расстояниях, является итерационным, и на каждой итерации необходимо вычислять матрицу расстояний между объектами. При большом количестве объектов это неэффективно и требует значительных вычислительных ресурсов. Вычислительная сложность первой итерации алгоритма k-means оценивается как O(kmn), где k, m и n — количество кластеров, признаков и объектов соответственно. Но итераций может быть много! Нам нужно сделать много проходов по набору данных.