Таким образом, взгляд пользователя направляется слева направо к изображению товара и кнопке «Купить». Использование переходов на главном экране может побудить клиента совершить целевое действие и создать общее впечатление о сайте и владельце компании.
Производная по направлению и градиент функции
В начале своей первой статьи о дифференцировании функции двух переменных я кратко объяснил концепцию частных производных первого порядка и подвел вас к сегодняшней теме. Так что же такое направленный дериватив? Вы уже знакомы с этим понятием по курсу 1, поскольку производную функции с одной переменной можно с уверенностью назвать направленной производной, так как она описывает скорость изменения функции. в направлении оси. .
И эта сущность, учитывая большее разнообразие направлений, распространяется на производные многомерных функций, особенно на производные от. Геометрически функция с двумя переменными обычно представляет собой поверхность, и мы четко ассоциируем значения «zet» с высотой. Таким образом, с геометрической точки зрения, скорость изменения этой функции — это скорость изменения высоты. Совершенно ясно, что «негоризонтальная» поверхность изменчива — в некоторых направлениях она крутая, в некоторых — плоская, а где-то — «плоская». А производная по направлению просто используется для характеристики «рельефа» (скорости изменения функции) в разных точках по разным направлениям. В связи с этим возникает первый вопрос:
а КАКИМ СПОСОБОМ вообще можно задать какое-то конкретное направление?
Помните забавную модель из урока «Предел функции с двумя переменными», где мы заходим в комнату в декартовой плоскости, а прямо над нами «висит потолок», заданный функцией. Рассмотрим один пункт его определения. В зависимости от выбора точки, мы имеем доступ к бесконечно малому «шагу» в некоторых или, что более вероятно, во всех направлениях. Направление традиционно задается радиусом, исходящим из точки и лежащим в плоскости. Сам луч может быть определен углом (между ним и осью или ), а еще лучше вектором.
как узнать скорость изменения функции в каком-либо направлении?
С производной в направлении. В качестве альтернативы можно использовать букву «ef» в обозначении: .
Если точка имеет производную по направлению луча (который выходит из точки и лежит в плоскости), то ее можно вычислить по следующей формуле:
— Некоторая производная 1-го порядка в точке; — Косинус направления (координаты вектора единичной длины), однозначно определяющий заданное направление.
Примечание: Направленная производная, конечно, не обязательно должна существовать во всех возможных направлениях (представьте, например, «пустой край»). Строгие условия его существования можно найти в руководстве.
На практике преобладает более компактное обозначение: .
— это ЧИСЛО, описывающее скорость изменения функции, с:
— если, то функция возрастает в точке вдоль определенного направления (поверхность «поднимается»),
— если, то функция убывает в точке вдоль указанного направления («наклон» поверхности),
— если, то функция постоянна в точке в заданном направлении (поверхность параллельна плоскости).
Грубо говоря, складываются измерение и сумма. Рассмотрим функцию с тремя переменными и точку, принадлежащую ее области определения.
Если производная существует в точке в направлении пространственного радиуса (начиная от точки), то она может быть вычислена по следующей формуле:
— частные производные трехпеременной функции в точке; — косинусы направления данного направления (они также являются соответствующими координатами вектора направления единичной длины) .
Наклон функции в точке — это отрезок, проведенный из точки и указывающий направление наиболее быстрого роста функции в этой точке.
И обещанный физический пример: рассмотрим функцию трех переменных, которая характеризует температуру пространственного тела в любой точке от. Тогда производная в одном или другом направлении в точке тела показывает скорость нагревания/охлаждения тела в соответствующих направлениях, а вектор показывает направление наиболее быстрого увеличения температуры в этой точке.
Это хороший и наглядный пример — а не какие-то надуманные электрические поля.
Давайте решим формулы с помощью некоторых задач:
Определите производную функции в точке по направлению вектора.
Не стесняйтесь, это пространственный вектор:
Алгоритм решения остается прежним. Вычислим частные производные порядка от 1 до. Именно в этот момент нам нужен глаз:
Найдите косинус направления:
И последний шаг:
Ответ:
Некоторые символические задачи, которые вы должны решить самостоятельно:
Определите производную функции в точке по направлению, составляющему равные углы с положительными полуосями координат.
Найдите направление и величину самого быстрого возрастания функции в точке.
Я не оставил никаких особых комментариев, так как все они очень похожи на примеры из первой части урока.
Аналогичным образом определите направленную производную и наклон для функций с несколькими переменными.
Поздравляем всех — сегодня мы не только выучили новый материал, но и обобщили понятие производной. мы можем забыть об этом, как о кошмаре. мы можем приступить к изучению интегралов, которых существует множество. …Я чувствую, что тебе грустно, поэтому решил поднять тебе настроение =)
Желаю вам выбрать правильное направление, которое, кстати, не ориентировано на склонности во всех аспектах жизни.
Благодарим вас за внимание и до скорой встречи!
Решения и ответы:
Пример 4: Решение: Вычислите частные производные 1-го порядка в точке: Определите косинусы направлений: Определите наклон функции в точке и вычислите ее длину: Это даст максимальный наклон области в точке: Ответ:
Пример 5: Решение: Вычислить частные производные 1-го порядка в точке: Вычислить наклон функции в точке и вычислить ее длину: Искомая направленная производная: Ответ:
Пример 7: Решение: вычислить частные производные 1-го порядка в точке:
Вот, собственно, и все базовые знания, необходимые для использования цветовых градиентов в веб-разработке. Но не все знают, что цветовые градиенты можно использовать и в других ситуациях. Вот их список.
Содержание
В трехмерном пространстве градиент скалярной функции является векторной функцией с компонентами
» width=»» height=»» />, » width=»» height=»» />, » width=»» height=»» />.
Или, для единичных векторов на ортогональных декартовых осях
<\partial x>\vec e_x + \frac <\partial \varphi> <\partial y>\vec e_y + \frac <\partial \varphi> <\partial z>\vec e_z.» width=»» height=»» />
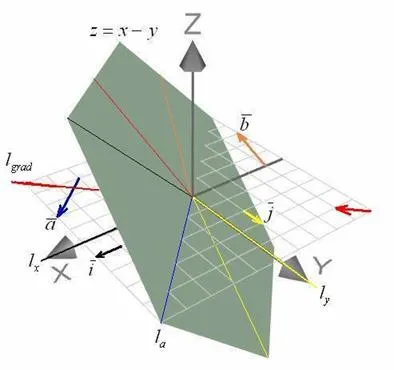
Если переменные, то их наклон
\?\ldots, \?\frac<\partial \varphi><\partial x_n>\right),» width=»» height=»» />
компоненты которого равны частным производным от
- Таким образом, размерность вектора градиента определяется размерностью пространства (или многообразия), в котором определено скалярное поле, градиент которого рассматривается.
- Оператор градиента (обычно, как упоминалось выше, или
Смысл градиента любой скалярной функции » width=»» height=»» /> дает суммарный дифференциал этой функции на соответствующее изменение координат в пространстве, в котором она определена, при сдвиге на. Если использовать одинаковые обозначения для обозначения функции от вектора и соответствующей функции от его координат, то можно написать:
\,dx_1 + \frac<\partial f><\partial x_2>\,dx_2 + \frac <\partial f><\partial x_3>\,dx_3 + \ldots = \sum_i \frac <\partial f><\partial x_i>\,dx_i = (\mathrm\,\mathbf \cdot d\mathbf x).» width=»» height=»» />
Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат » width=»» height=»» /> — является вектором, то вычисленный обычным способом градиент оказывается ковариантным вектором, т.е. вектором, записанным в двойственном базисе, который может дать масштаб, только если просто сложить суммы обычных (антидифференциальных) координат, т.е. вектор, записанный в обычном базисе. Таким образом, выражение (вообще говоря, для произвольных кривых координат) может быть записано вполне корректно и неизменно следующим образом:
Или, согласно правилу Эйнштейна, можно опустить знак суммы,
(на ортонормальном базисе мы можем записать все индексы меньшими, как мы это делали выше). Однако градиент оказывается истинным ковариантным вектором во всех криволинейных координатах.
В различных областях физики используется понятие градиента различных физических полей.
Например, напряженность электростатического поля равна минус градиент электрического потенциала, а напряженность гравитационного поля (ускорение свободного падения) в классической теории гравитации равна минус градиент гравитационного потенциала. Сила в классической механике — это сила минус градиент потенциальной энергии.
Понятие градиента применяется не только в физике, но и в смежных и даже сравнительно далеких от физики науках (иногда это применение количественное, а иногда только качественное).
Например, градиент концентрации — увеличение или уменьшение концентрации растворенного вещества в любом направлении, градиент температуры — увеличение или уменьшение температуры среды в любом направлении и т.д.
Градиент этих величин может иметь различные причины, например, механический барьер, влияние электромагнитных, гравитационных или других полей, или разница в растворимости соседних фаз.
Геометрический смысл
Рассмотрим семейство линий уровня функции
Нетрудно показать, что градиент функции ^0″ width=»» height=»» /> перпендикулярен её линии уровня, проходящей через эту точку. Модуль градиента показывает максимальную скорость изменения функции в окрестности ^0″ width=»» height=»» />т.е. частота линий уровня. Например, на топографических картах изображены контурные линии, коэффициент наклона которых указывает крутизну склона или подъема в данной точке.